一、文章标题
可微与连续的关系
二、文章内容
在数学中，可微和连续是两个重要的概念，它们在微积分学中扮演着重要的角色。可微性是函数局部性质的一种表现，而连续性则是函数整体性质的基础。本文将探讨可微与连续之间的关系。
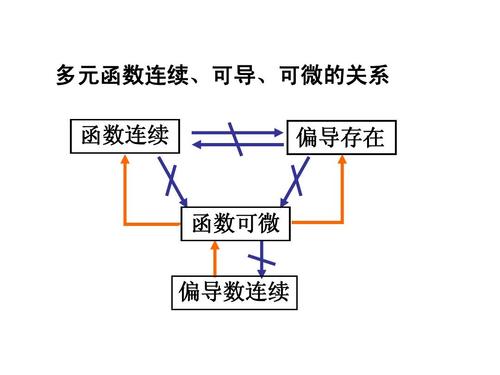
1. 连续与可微的定义
首先，我们来了解一下连续和可微的定义。连续是指函数在定义域内的任意一点处都有定义，且在该点处的函数值与其极限值相等。而可微则是指函数在某一点处存在导数，即函数在该点处的切线斜率存在。换句话说，如果函数在某一点处连续，那么该函数在该点处就有可能可微。
2. 可微必连续
可微是连续的必要条件。如果函数在某一点处不连续，那么它肯定在该点处不可微。这是因为，可微的前提是函数在某一点附近存在明确的导数和切线斜率，如果该点不连续，则这些性质将不存在。因此，我们可以通过检查函数的连续性来判断其是否可微。
3. 连续未必可微
然而，值得注意的是，连续的函数不一定可微。在某些情况下，尽管函数在某一点处是连续的，但由于存在拐点或尖点等特殊情况，导致函数在该点处不可导或无法求出明确的切线斜率。例如，绝对值函数在原点处是连续的，但不可导。这说明我们在判断函数的可微性时，还需要综合考虑其他因素。
4. 可微与连续的关系总结
综上所述，可微与连续之间存在着密切的关系。首先，可微是连续的必要条件，即如果函数在某一点处不连续，那么它肯定不可微。然而，连续的函数未必可微，因为可能存在一些特殊情况导致无法求出明确的导数或切线斜率。因此，在研究函数的性质时，我们需要综合考虑其连续性和可微性。
在实际应用中，我们常常会遇到需要求解导数或进行微积分运算的问题。这时，我们需要先判断函数的连续性和可微性，以确保我们的计算过程和结果都是合理的。同时，了解可微与连续的关系也有助于我们更好地理解函数的性质和特点，为进一步的学习和研究打下基础。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
