一、标题
关于拟合函数的理解与应用
二、内容
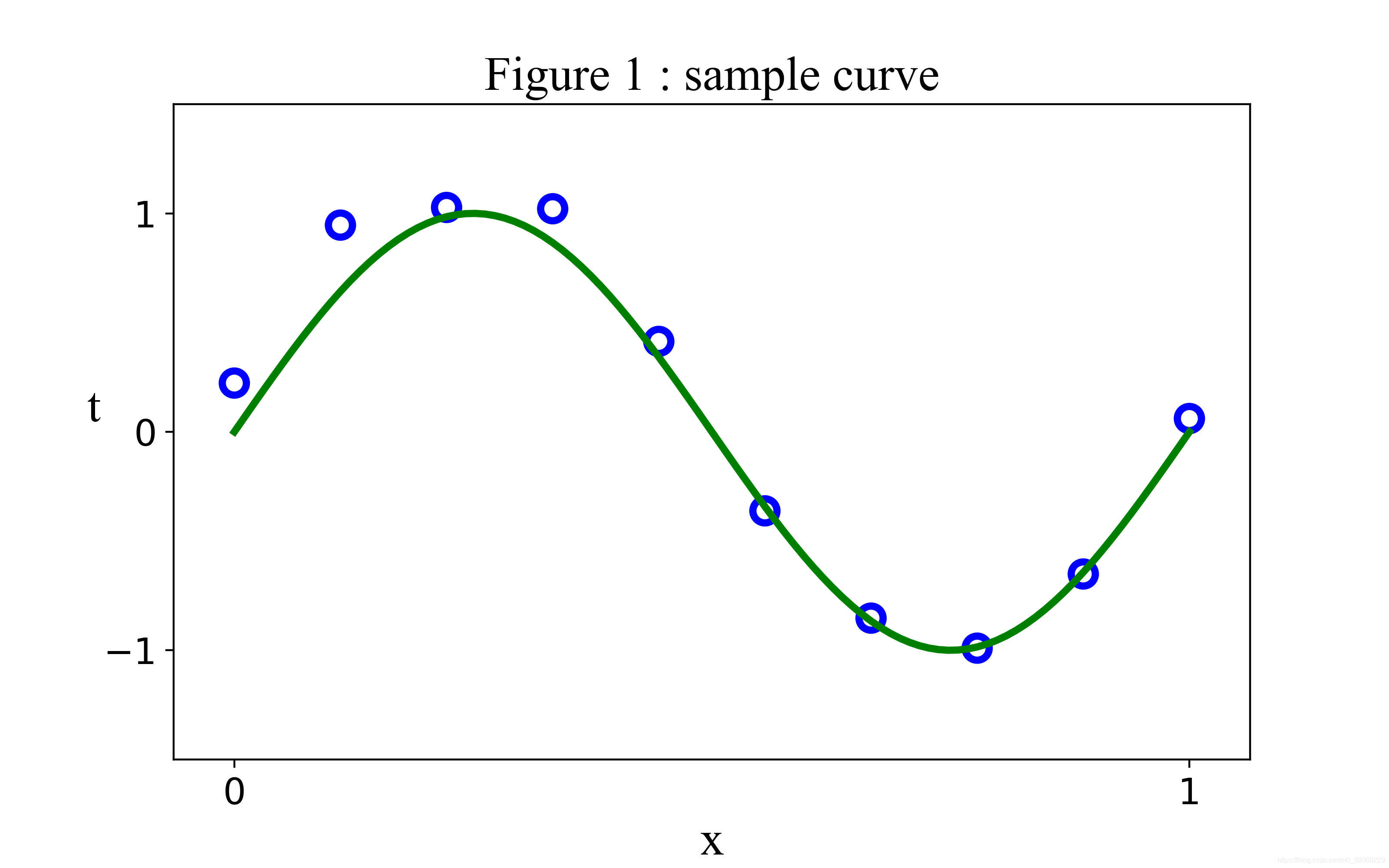
在数学领域，拟合函数是一种重要的概念，它常常被用于对一组数据进行处理和建模。通过拟合函数，我们可以将一组数据通过数学模型进行表示，从而更好地理解数据的特征和规律。本文将深入探讨拟合函数的基本概念、方法及其应用。
1. 拟合函数的基本概念
拟合函数是数学建模中常用的一个概念，主要用于对数据进行曲线拟合或插值计算。在实际应用中，拟合函数经常使用各种形式的曲线来对数据进行近似表达。这种曲线可能是线性或非线性的，也可能包含多种不同种类的曲线和数学公式。无论采用哪种形式，拟合函数的目的是尽可能地让数据点在拟合曲线上或其附近，以实现对数据的最佳近似。
2. 拟合函数的方法
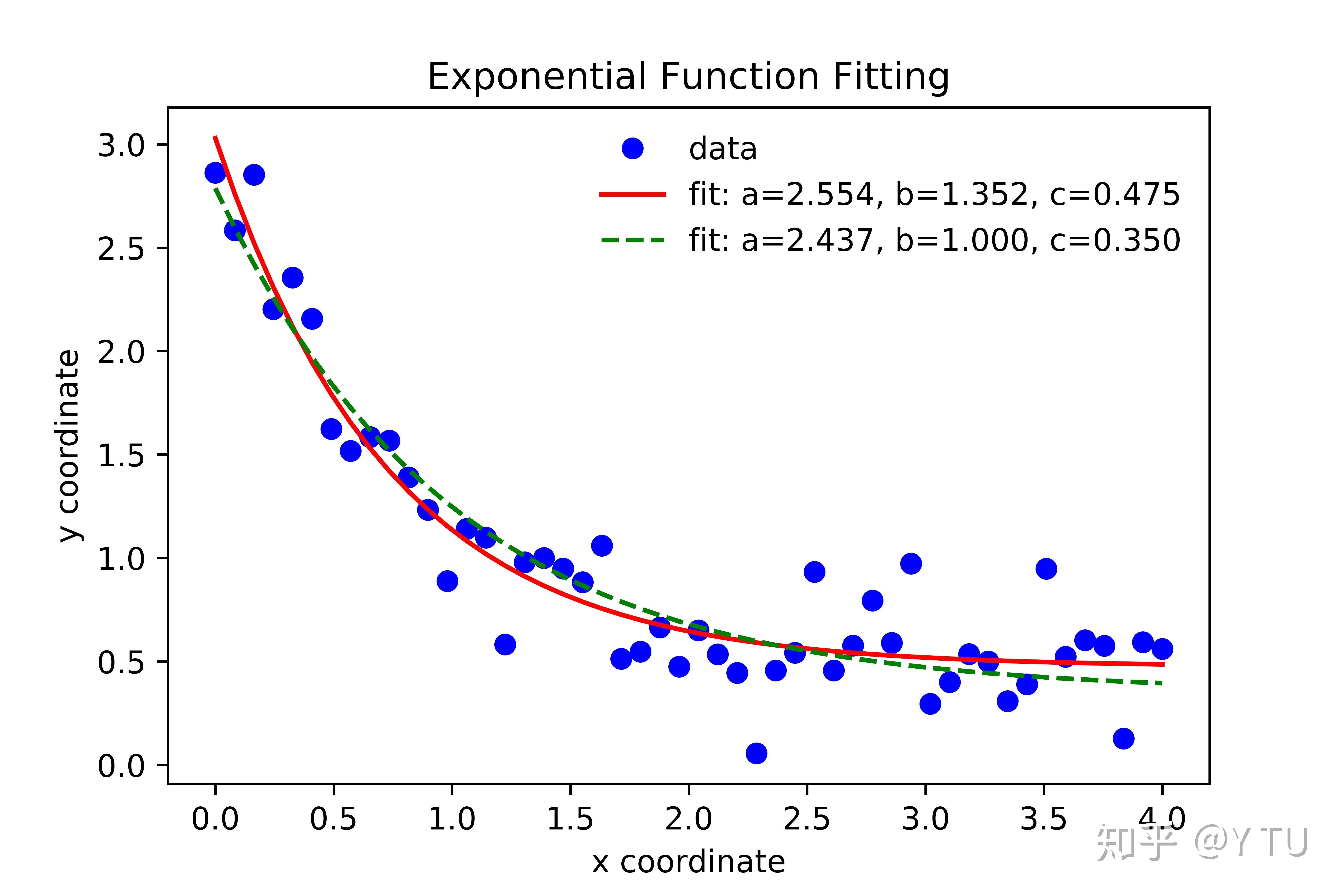
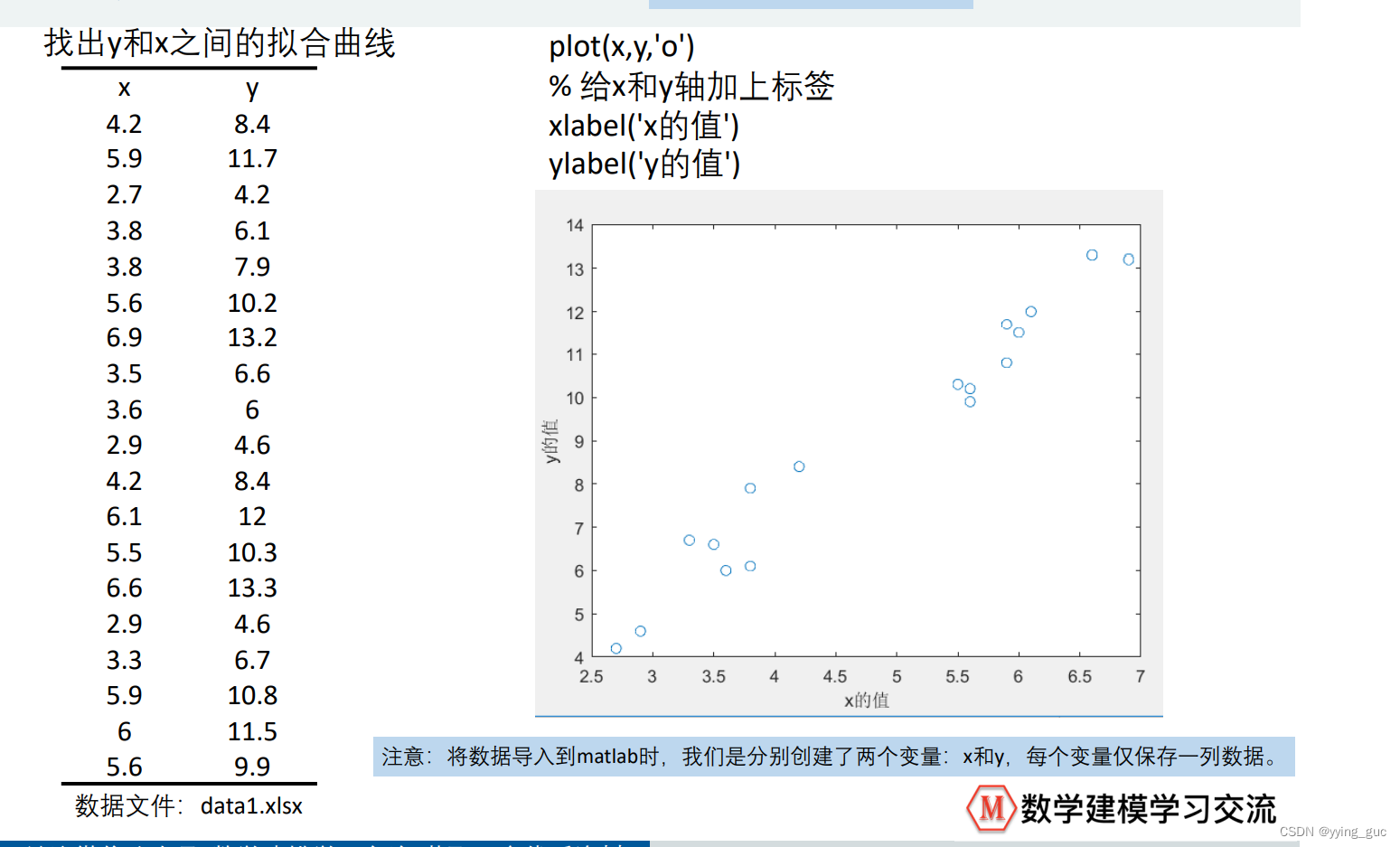
拟合函数的方法多种多样，常见的包括线性回归、多项式回归、指数回归等。这些方法各有其特点和适用场景。例如，线性回归适用于数据点之间存在线性关系的情况；多项式回归则适用于数据点之间存在非线性关系，但可以用多项式形式进行近似的场合；指数回归则用于数据变化呈指数形态的场合。在应用拟合函数时，应根据具体数据情况选择最合适的拟合方法。
此外，对于离散数据点，除了常规的拟合方法外，还有插值方法可以用来填充缺失的或不可见的值。例如，我们可以利用牛顿插值法、拉格朗日插值法等方法对离散数据进行插值计算。
3. 拟合函数的应用
拟合函数在各个领域有着广泛的应用。在金融领域，拟合函数常被用于预测股票价格、汇率等金融指标的变化趋势；在工程领域，它被用于预测设备性能、模拟系统运行等；在医学领域，它被用于研究生物指标与药物剂量之间的关系等。通过使用拟合函数，我们可以更好地理解数据的特征和规律，从而为决策提供科学依据。
总之，拟合函数是数学建模中一个重要的概念，它具有广泛的应用场景和重要的应用价值。通过学习和掌握拟合函数的基本概念、方法和应用，我们可以更好地理解和处理数据，从而为实际应用提供有力支持。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
