文章标题：多项式拟合
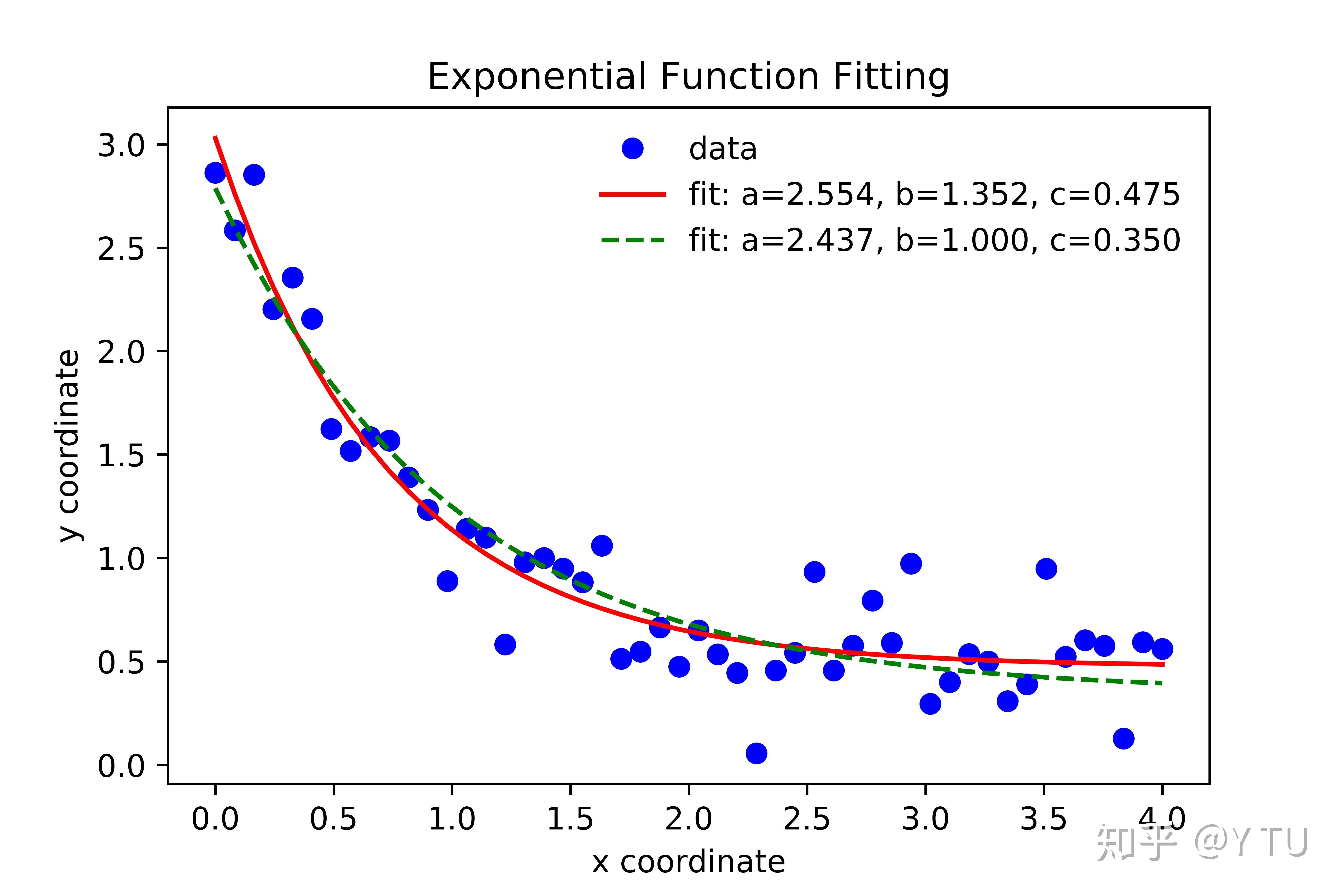
一、引言
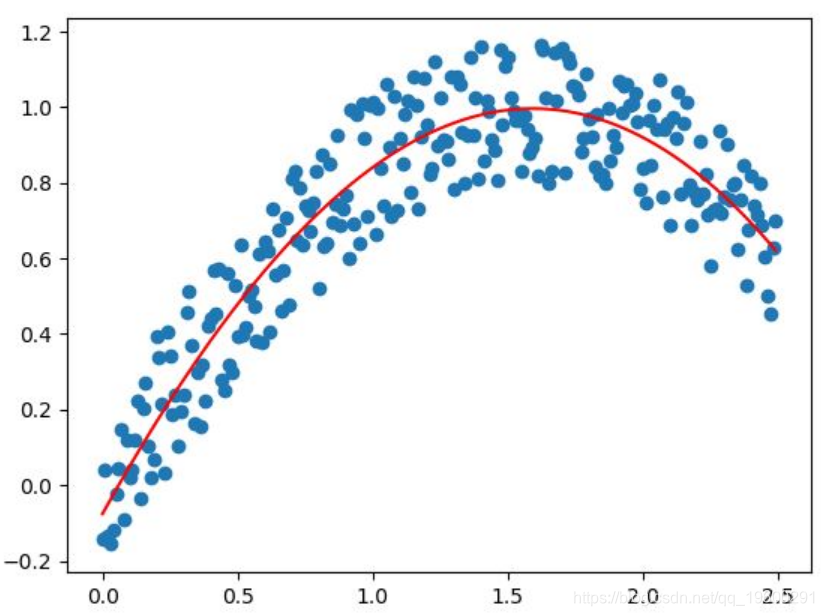
在数学和科学计算中，多项式拟合是一种常用的方法，用于根据一组已知的数据点来估计或预测未知的数据点。多项式拟合通常用于数据建模、插值和逼近等领域。本文将介绍多项式拟合的基本概念、方法以及应用场景。
二、多项式拟合的基本概念
多项式拟合是一种通过最小化误差平方和来找到最佳拟合多项式的方法。具体来说，给定一组数据点（x, y），我们希望找到一个多项式函数f(x)，使得该函数在所有数据点上的误差平方和最小。这个多项式函数被称为最佳拟合多项式。
三、多项式拟合的方法
四、多项式拟合的应用场景
多项式拟合在许多领域都有广泛的应用，如科学计算、数据处理、图像处理等。例如，在气象学中，我们可以通过多项式拟合来预测未来某一天的天气情况；在图像处理中，我们可以通过多项式拟合来对图像进行平滑或去噪等操作；在经济学中，我们可以通过多项式拟合来分析经济增长的趋势等。
五、结论
多项式拟合是一种重要的数学方法，它具有广泛的应用场景和重要的实际意义。通过使用适当的多项式拟合方法，我们可以更好地理解和分析数据之间的关系，并做出更准确的预测和决策。未来随着科技的不断发展和进步，多项式拟合将在更多领域得到应用和推广。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
