中序遍历
中序遍历是一种树(二叉树)遍历方式,按照树的层次遍历。先遍历左子树,然后访问根节点,最后遍历右子树。对于任何一个给定的二叉树,其各个节点都是按这样的顺序一一被访问。本文将简要介绍中序遍历的相关知识及其实际应用。
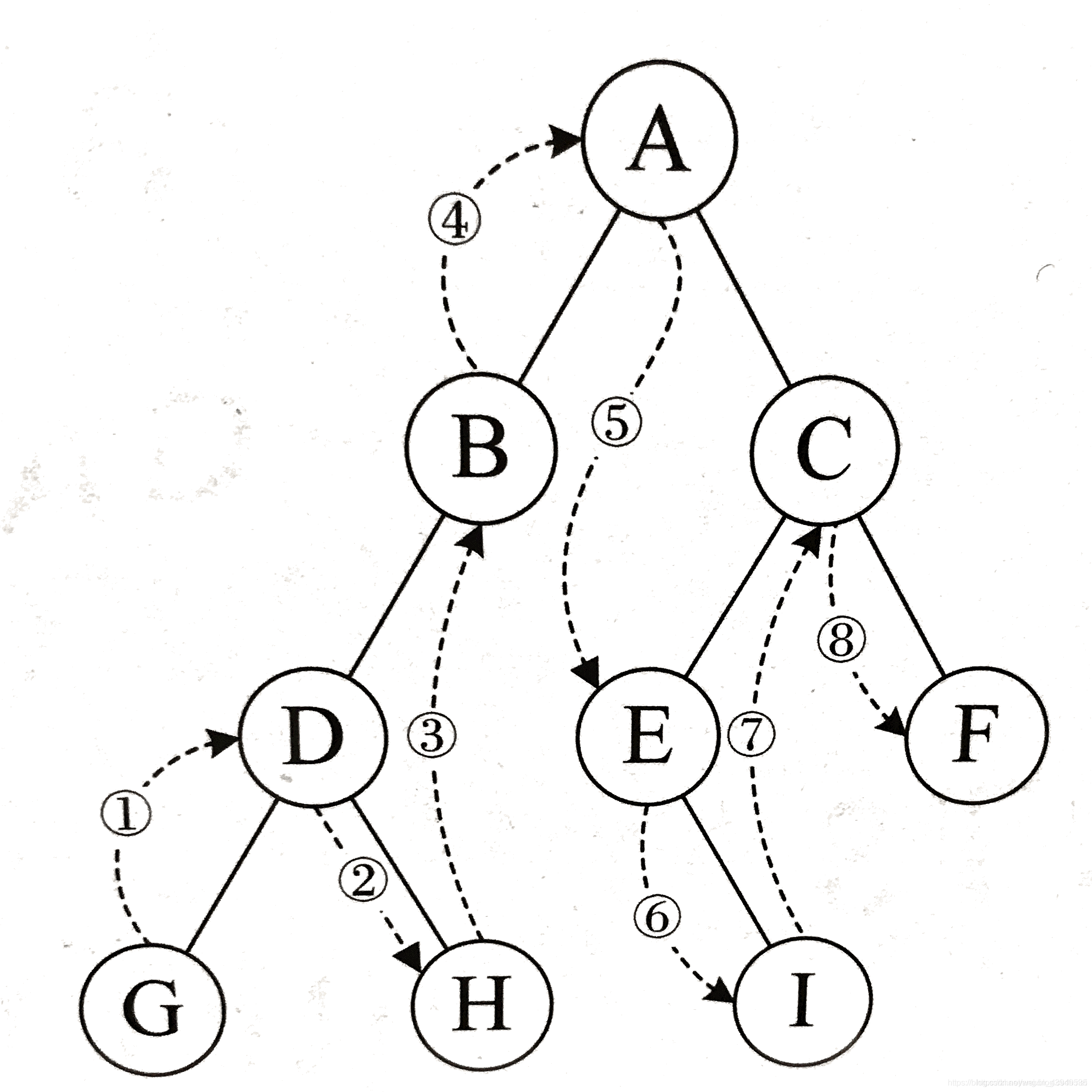
一、基本概念
首先,中序遍历是指沿着树的左、右子树(根节点的顺序)的顺序进行的遍历方式。这个顺序的重要性在于它能更好地反映出树的结构信息,对于某些问题(如二叉搜索树)的解决特别有帮助。
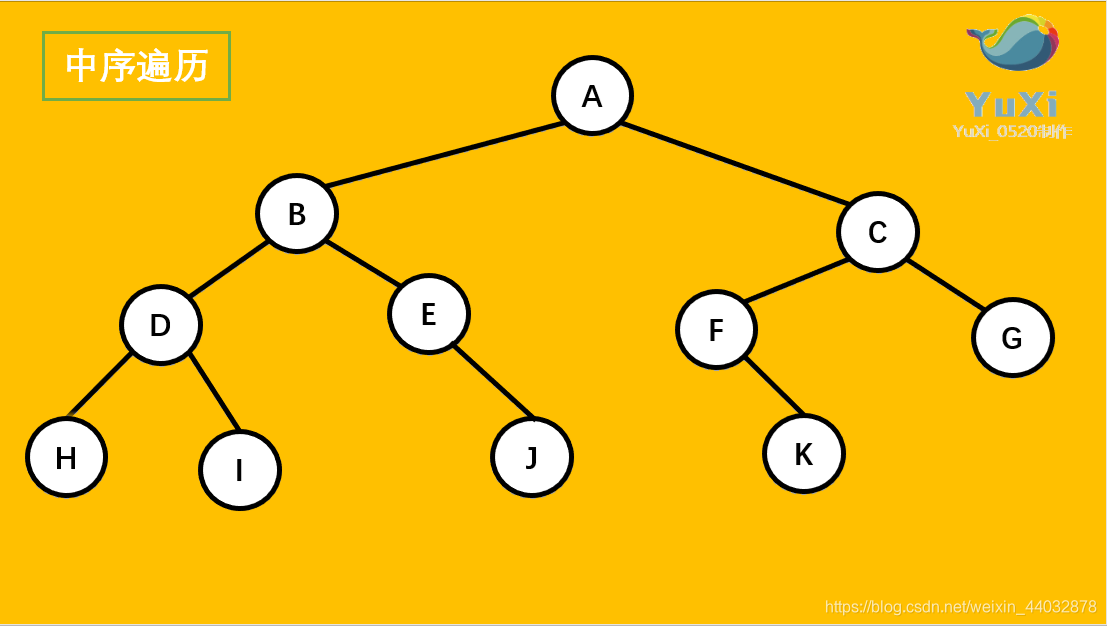
二、中序遍历的步骤
中序遍历的步骤可以归纳为:
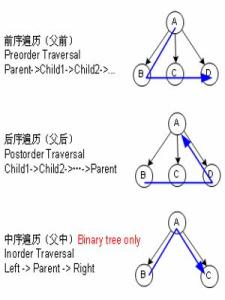
- 如果当前节点存在,先进行递归地左子树的中序遍历;
- 然后访问当前节点;
- 最后递归地右子树的中序遍历。
具体操作上,我们可以使用递归或非递归的方式来进行中序遍历。
三、中序遍历的应用场景
- 树的打印:对于任意一个二叉树,我们可以使用中序遍历的方式打印出节点的顺序序列。这对于了解树的层次结构非常有帮助。
- 排序和搜索:在二叉搜索树(BST)中,中序遍历可以得到一个升序序列,所以经常用于查找、插入或删除元素的操作。因为你知道树的每一个节点的左子树都比节点本身小,右子树都比节点本身大,这有助于我们更有效地搜索和排序。
- 深度优先搜索:中序遍历也可以看作是一种深度优先搜索的算法,这可以帮助我们找到最短的路径或者解决一些需要深度优先搜索的问题。
四、中序遍历的代码实现
在编程语言中,我们可以使用递归或非递归的方式来实现中序遍历。这里以Python为例,展示递归实现的方式:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def inorder_traversal(root):
if root: # 如果根节点存在
inorder_traversal(root.left) # 递归左子树的中序遍历
print(root.val) # 访问当前节点
inorder_traversal(root.right) # 递归右子树的中序遍历
以上就是关于中序遍历的基本概念、步骤、应用场景和代码实现。通过了解并掌握这一算法,我们可以更好地理解二叉树的结构和特性,为解决相关问题提供有效的解决方案。






















