文章标题：trapz——一个数值积分工具的解析
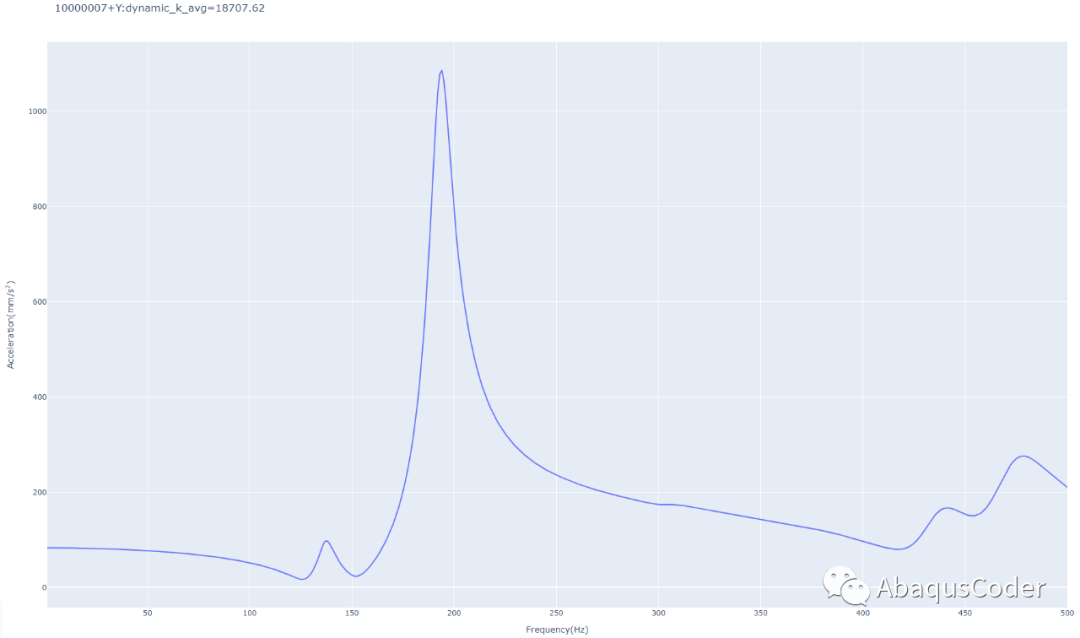
在科学计算和数据分析中，数值积分是一种常用的数学方法。而trapz正是这种计算中的一种工具，用于求解定积分的近似值。那么，什么是trapz呢？
一、trapz的定义
trapz，全称为“梯形求积法”，是一种用于求解定积分的方法。其基本思想是将被积函数在积分区间内近似为一系列梯形的面积之和，然后求和这些梯形的面积来得到定积分的近似值。
二、trapz的使用方法
使用trapz进行数值积分通常需要两个步骤：首先确定积分的上下限，其次将被积函数转换为相应的梯形面积函数。之后利用计算机程序（如Python中的NumPy库）对区间进行分割并计算各小段上的梯形面积，最后将所有小段上的梯形面积相加，即可得到定积分的近似值。
三、trapz的优点和局限性
优点：
局限性：
四、trapz的应用场景
trapz广泛应用于各种科学计算和数据分析中，如物理、工程、经济等领域。例如，在物理学中，trapz可以用于求解物体的质量、重心等物理量；在工程领域中，可以用于求解复杂的工程问题中的能量、功率等参数；在经济学中，可以用于计算收益、成本等经济指标的积分值。
总之，trapz作为一种常用的数值积分工具，具有简单易用、精度可调等优点，在科学计算和数据分析中发挥着重要作用。但是，在使用时也需要注意其局限性，根据具体情况选择合适的数值积分方法。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
