一、文章标题
什么是逆矩阵？
二、文章内容
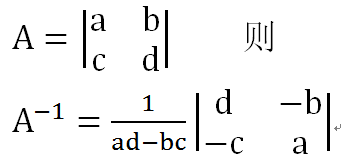
在数学领域，逆矩阵是一个非常重要的概念，特别是在线性代数和矩阵理论中。那么，什么是逆矩阵呢？接下来我们将一起探讨这个问题。
1. 矩阵的基本概念
首先，我们需要了解什么是矩阵。矩阵是一个由数字组成的矩形阵列，行和列的数量可以不同。在数学运算中，矩阵可以执行各种操作，如加法、减法、数乘等。
2. 逆矩阵的定义
逆矩阵，也称为倒数矩阵，是相对于一个给定矩阵而言的。如果存在一个矩阵B，使得对于任何矩阵A，有AB=BA=E（E为单位矩阵），那么我们称B为A的逆矩阵。简单来说，一个矩阵的逆矩阵是与之相乘得到单位矩阵的另一个矩阵。
3. 逆矩阵的存在条件
不是所有的矩阵都有逆矩阵。一个矩阵有逆矩阵的条件是它的行列式不为零，并且它的秩等于其未定义行数或列数。也就是说，只有方阵才可能存在逆矩阵。此外，对于不可逆或奇异矩阵，我们需要其他的方法进行计算或求解。
4. 逆矩阵的计算方法
计算逆矩阵通常需要用到高斯消元法或者行列式等方法。对于一般的二阶方阵，我们可以通过行列式与伴随矩阵的关系直接求解；对于更高阶的方阵，则需通过更复杂的算法进行计算。然而，在许多计算机编程语言和软件中，提供了专门求解逆矩阵的函数和工具，我们只需调用即可。
5. 逆矩阵的应用
逆矩阵在许多领域有着广泛的应用。例如，在物理、工程和计算机科学中，我们需要解线性方程组或求解系统的动态变化等问题时，就需要使用到逆矩阵的概念和计算方法。此外，在图像处理、信号处理和统计等领域中，逆矩阵也扮演着重要的角色。
总之，逆矩阵是线性代数和矩阵理论中的重要概念。通过了解其定义、存在条件、计算方法和应用领域，我们可以更好地理解其在各个领域中的应用和重要性。希望这篇文章能够帮助你更好地理解逆矩阵这一概念。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
