初等矩阵
一、引言
在数学领域，矩阵是一个非常重要的概念，它被广泛应用于线性代数、图像处理、数值分析等各个领域。而其中，初等矩阵更是线性代数的基础概念之一，其在许多复杂计算中都起到了不可或缺的作用。
二、什么是初等矩阵
初等矩阵是矩阵在经过有限次初等变换后得到的矩阵。这些初等变换包括：交换两行（或两列）的位置、某行（或列）乘以一个非零常数、某行（或列）的倍数加到另一行（或列）。通过这些变换，我们可以得到初等矩阵。
三、初等矩阵的分类
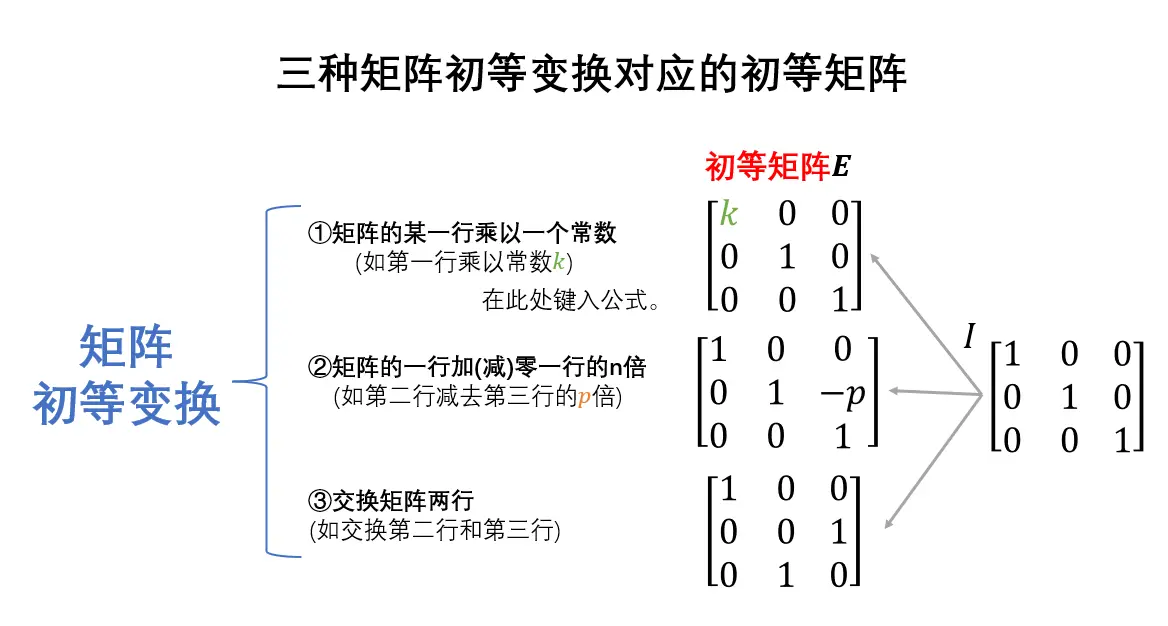
根据初等变换的不同，初等矩阵可以分为三种类型：
四、初等矩阵的应用
初等矩阵在数学计算中有着广泛的应用。例如，在求解线性方程组时，我们常常需要用到初等变换来简化计算过程。此外，在图像处理、数值分析等领域，初等矩阵也扮演着重要的角色。
五、总结
初等矩阵是线性代数中一个重要的概念，它通过有限次初等变换得到新的矩阵。这些初等变换包括交换行（或列）、缩放行（或列）以及线性组合行（或列）。通过这些变换，我们可以简化复杂的计算过程，提高计算的效率。同时，初等矩阵在图像处理、数值分析等领域也有着广泛的应用。因此，对于学习线性代数的学生来说，掌握初等矩阵的概念和性质是非常重要的。
总的来说，初等矩阵是数学中一个基础而重要的概念，它在各个领域都有着广泛的应用。希望通过这篇文章，读者能够对初等矩阵有更深入的理解和认识。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
