统计量
一、统计量的概念
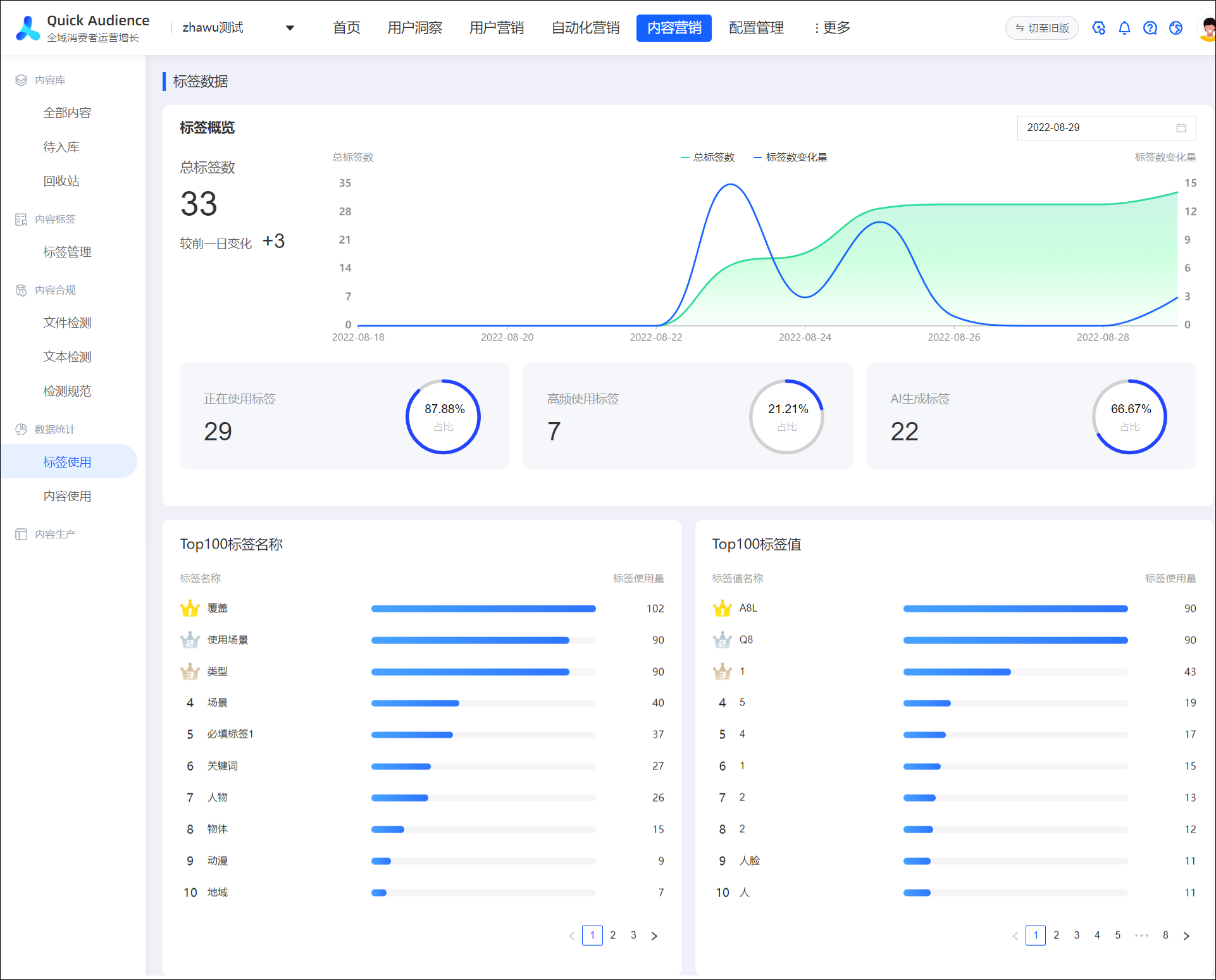
在统计学中,统计量是一个重要的概念,它是对一组数据进行分析和推断的基石。那么,什么是统计量呢?

统计量是样本数据的抽象表达,是用于描述样本或总体特征的量化指标。通过对样本数据的观察和计算,我们可以得到一系列的统计量,如平均数、中位数、众数、方差、标准差等。这些统计量不仅可以帮助我们了解数据的分布特征,还可以用于推断总体的性质。

二、常见统计量的介绍
- 平均数(Mean):平均数是所有数据之和除以数据的个数,它反映了数据的平均水平。但需要注意的是,平均数容易受到极端值的影响。
- 中位数(Median):将一组数据按照大小顺序排列后,位于中间位置的数值即为中位数。中位数不易受极端值的影响,更能反映数据的中心趋势。
- 众数(Mode):在一组数据中出现次数最多的数值即为众数,它可以反映数据的集中趋势。
- 方差(Variance):方差是各个数据与平均数之差的平方的平均数,它反映了数据的离散程度。
- 标准差(Standard Deviation):标准差是方差的平方根,它同样反映了数据的离散程度,但相较于方差更易于理解。
三、统计量的应用
统计量在日常生活和科学研究中有着广泛的应用。例如,在市场调研中,我们可以通过分析消费者的消费数据,得到平均消费水平、消费的离散程度等信息,从而为企业的市场策略提供参考。在科学研究领域,统计量更是不可或缺的工具,通过对实验数据的统计分析,科学家们可以推断出总体的性质,从而得出科学的结论。
总之,统计量是统计学中的重要概念,通过对样本数据的统计分析,我们可以了解数据的分布特征和总体性质,为决策提供科学依据。因此,掌握统计量的概念和应用是非常重要的。
以上就是关于统计量的基本介绍和部分应用场景的概述,希望对你有所帮助。当然,统计学是一个非常庞大和复杂的学科领域,还有许多其他的统计量和概念等待我们去学习和探索。



















