一、文章标题
标准差函数：定义、计算与应用
二、文章内容
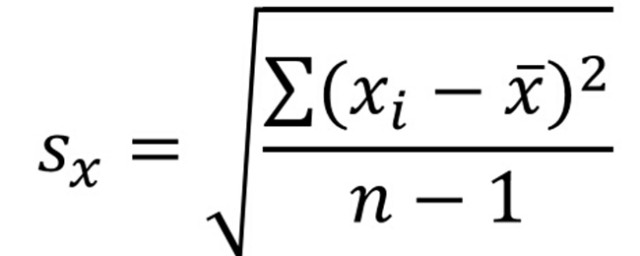
一、标准差函数的定义
在统计学中，标准差函数是一个重要的数学概念，它反映了数据集的离散程度或分布情况。简单来说，标准差是用于度量数据点相对于其均值的波动大小的一种指标。它主要用于衡量一组数值的离散程度，也就是数值之间的差异程度。
二、标准差函数的计算
标准差函数的计算通常需要用到样本的均值和每个数据点与均值之差的平方的均值，然后再对这种平均值的平方根进行计算。这里需要注意的是，不同的场景可能会涉及到不同类型的标准差函数（如样本标准差和总体标准差）。具体的计算公式因应用场景而异。
三、标准差函数的应用
四、总结
总的来说，标准差函数是一个非常重要的统计工具，它可以帮助我们了解数据的分布情况、波动情况以及风险水平等重要信息。无论是对于科研工作者还是普通用户，掌握标准差函数的定义和计算方法都是非常必要的。同时，我们也需要注意到，不同的应用场景可能需要采用不同的标准差函数，我们需要根据实际情况进行选择和运用。
以上是我对标准差函数的简单介绍和讲解，希望能对您有所帮助。由于Markdown格式的局限性，无法直接展示出更多的图表和实例，如有需要可以查阅相关书籍或在线资源进行深入学习。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
