文章标题：双精度浮点数
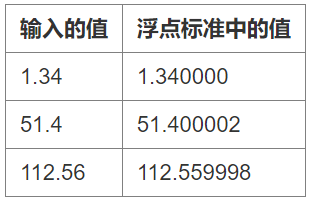
在计算机科学中，双精度浮点数是一种常用的数值数据类型，用来存储含有小数部分的数字。对于我们平常的工作与学习来说，掌握和理解双精度浮点数的原理与特性至关重要。
一、双精度浮点数的定义
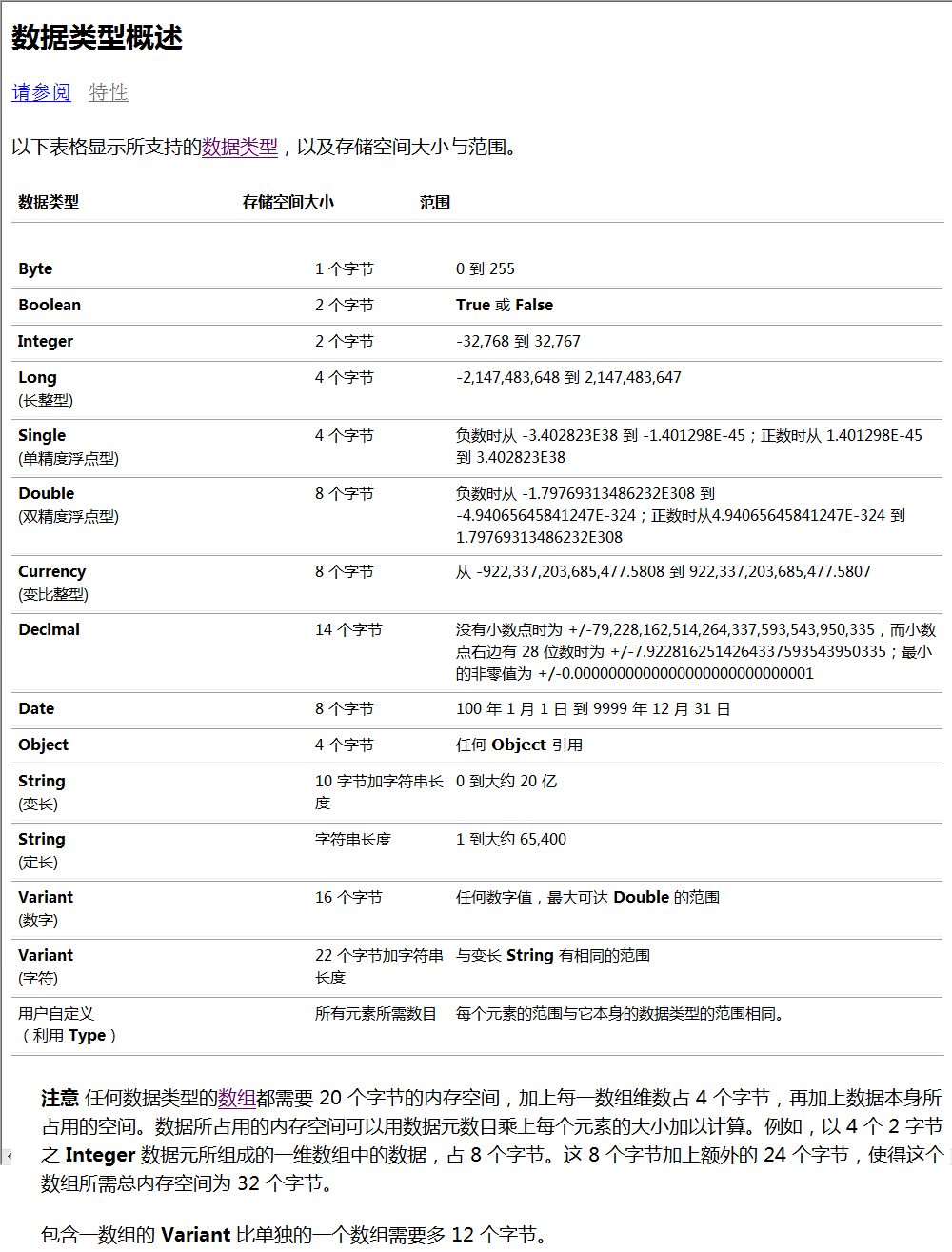
双精度浮点数通常是指一个能够表示更大数值范围、具有更多有效数字的高精度浮点数。其数据结构包括符号位、指数位和尾数位三个部分，主要应用于需要高精度的计算领域，如科学计算、图形图像处理等。
二、双精度浮点数的特点
三、应用领域
双精度浮点数被广泛用于许多重要的科学领域。如需要处理高精度数据计算的研究领域（物理、化学、金融等）、图形图像处理领域（如三维动画制作）、工程设计和计算机辅助设计（CAD）等。此外，双精度浮点数也用于其他一些需要高精度的应用场合，如卫星导航定位、加密算法等。
四、使用注意事项
尽管双精度浮点数在许多方面都有优势，但也要注意其使用可能带来的问题。由于双精度浮点数的计算过程涉及到复杂的数学运算和计算机硬件支持，因此需要谨慎处理可能出现的数据溢出、舍入误差等问题。同时，双精度浮点数的计算过程也可能会比其他类型的数据类型更消耗计算机资源。因此，在实际应用中，需要根据具体需求和场景来选择合适的数据类型。
综上所述，双精度浮点数是一种重要的数据类型，具有高精度、宽的数值范围等特点，在许多领域都有广泛的应用。然而，在使用过程中也要注意其可能带来的问题，确保数据的准确性和有效性。通过理解和掌握双精度浮点数的原理和特性，我们可以更好地应用它来处理和解决实际问题。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
