一、文章标题
log函数图像详解
二、文章内容
在数学中，对数函数是一种非常重要的基本函数。其图像常常出现在数学学习中，那么我们今天就来看看log函数图像是什么样子以及如何生成。
首先，让我们了解下什么是log函数。对数函数，也称为对数曲线，是反函数的一种，用于表示指数函数的逆运算。它的一般形式为y=log(a)x（其中a为底数），以e为底的对数记作ln。当a是自然数时，a为对数的底数。通过该函数可以解决各种形式的数学问题，而其图像也是十分有趣和有意义的。
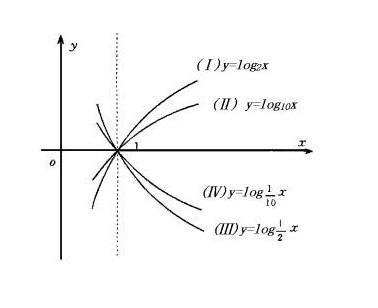
当我们使用图像软件来绘制log函数的图像时，我们可以观察到log函数图像的一些基本特征。首先，对数函数的图像是一个弯曲的曲线，与指数函数的直线图像完全不同。对于不同的底数a，log函数的图像也会有所不同。当a大于1时，函数上升并最终在某个水平线y轴上停止增长。如果a大于零且不等于一但小于1，图像则是连续下滑且渐进向零轴上，同时在二维图形的展现下越来越趋于极限位置的水平线上增长或平缓过度以直达到整个右边缘趋势的增长极线形近直至渐进完全变化形成统一类带状形态的图像。
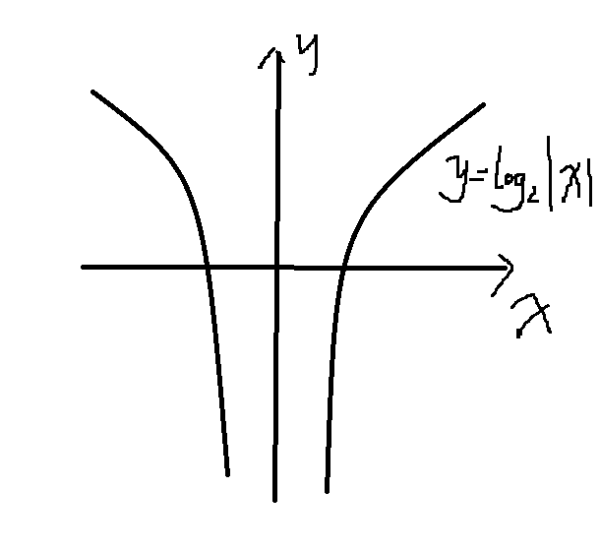
（1）在x轴正方向上无限增长：当x的值趋向于正无穷时，y值无限增加，图像向着正方向上水平延伸； （2）零点和曲线形态：图像通常会在x=1的点有一个极小值或顶点；当底数大于1时，曲线的形态呈向上凸起的弧形；而当底数小于1但大于0时，曲线则是向下凹的； （3）与指数函数的对称性：对于底数大于1的对数函数和其对应的指数函数，它们的图像在图形上具有对称性。当以e为底数的对数（自然对数）和对应的指数（自然指数）相加等于y轴时也称为负对称点线而图形被称为统一关系轴对或L式图案一般相互交换交替成为平面两色构形轮廓的整体坐标元素其中x的因次区间关于其负数的图形都是相对独立的在X轴左右两边展开进行平行式排布，其呈现为"Z"字形变化特征并因此有助在平面上得到稳定的定向几何状态描述.
以上就是关于log函数图像的一些基础信息了。在实际学习中我们应当根据需要绘制不同底数的对数函数图像，从而更深入地理解其特性与性质。通过掌握log函数的特性与技巧，我们可以更好地运用它在解决实际问题中。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
