一、文章标题
z统计量
二、文章内容
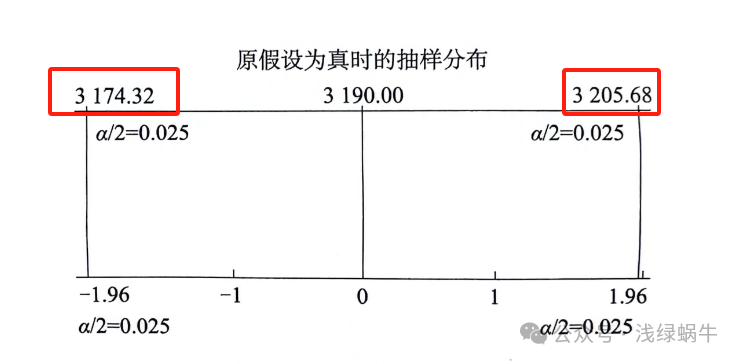
z统计量是统计学中常用的一个概念，用于描述正态分布中两个变量之间的差异程度。在统计分析中，z统计量常被用来进行假设检验、置信区间估计等。下面我们将详细介绍z统计量的概念、性质及计算方法。
一、z统计量的概念
z统计量是一种标准化的统计量，通常用于比较一个样本均值与总体均值之间的差异程度。它以标准差为单位的测量值，可用于判断样本结果是否与预期值或假设值显著不同。z统计量的值一般基于正态分布计算得出，正态分布是统计学中最常见的分布类型之一。
二、z统计量的性质
标准化：z统计量是一种标准化的统计量，它的值不受样本大小、计量单位等因素的影响，使得不同样本之间的比较变得更为方便。
适用范围广：z统计量适用于大样本情况，当样本量足够大时，可以认为样本服从正态分布，此时z统计量的计算结果较为准确。
概率解释：z统计量的值可以在正态分布表中查找对应的概率值，从而进行假设检验、置信区间估计等统计分析。
三、z统计量的计算方法
z统计量的计算方法相对简单，一般包括以下几个步骤：
计算样本均值和样本标准差；
根据总体均值和标准差（或已知的假设值）计算标准化值；
将标准化值转换为z统计量的值。
具体来说，z值的计算公式为：z = (样本均值 - 总体均值) / 样本标准差。当总体标准差未知时，可以使用样本标准差代替。z值的绝对值越大，说明样本均值与总体均值的差异程度越大。
四、z统计量的应用场景
z统计量在统计学中有着广泛的应用场景，例如在假设检验、置信区间估计、回归分析等方面都有所应用。在假设检验中，z统计量常用于检验两个样本之间的差异是否显著；在置信区间估计中，z统计量可用于估计总体参数的置信区间；在回归分析中，z统计量可用于判断回归系数的显著性等。
总之，z统计量是统计学中一个重要的概念，它能够帮助我们更好地理解数据之间的关系和差异程度。在实际应用中，我们需要根据具体的研究目的和数据特点选择合适的统计分析方法，并正确地运用z统计量进行相关分析。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
