文章标题：数值积分
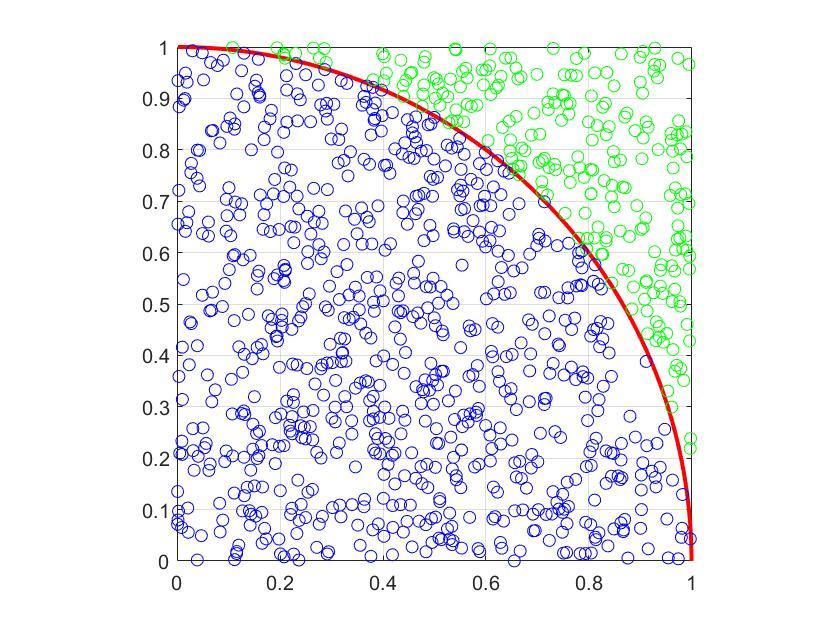
一、引言
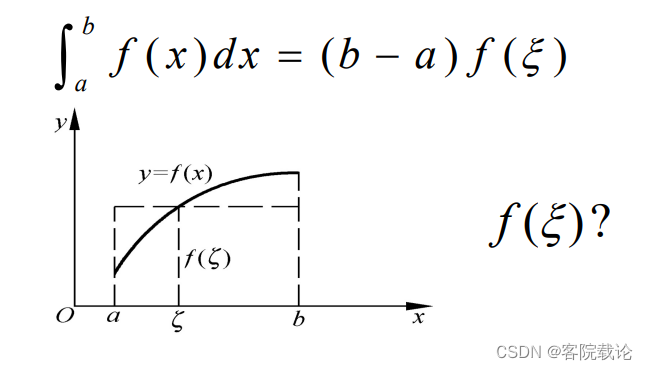
数值积分是数学中一个重要的概念，广泛应用于科学计算和工程领域。它涉及到对函数进行积分运算，通过数值方法近似求解定积分的值。本文将介绍数值积分的基本概念、方法以及应用。
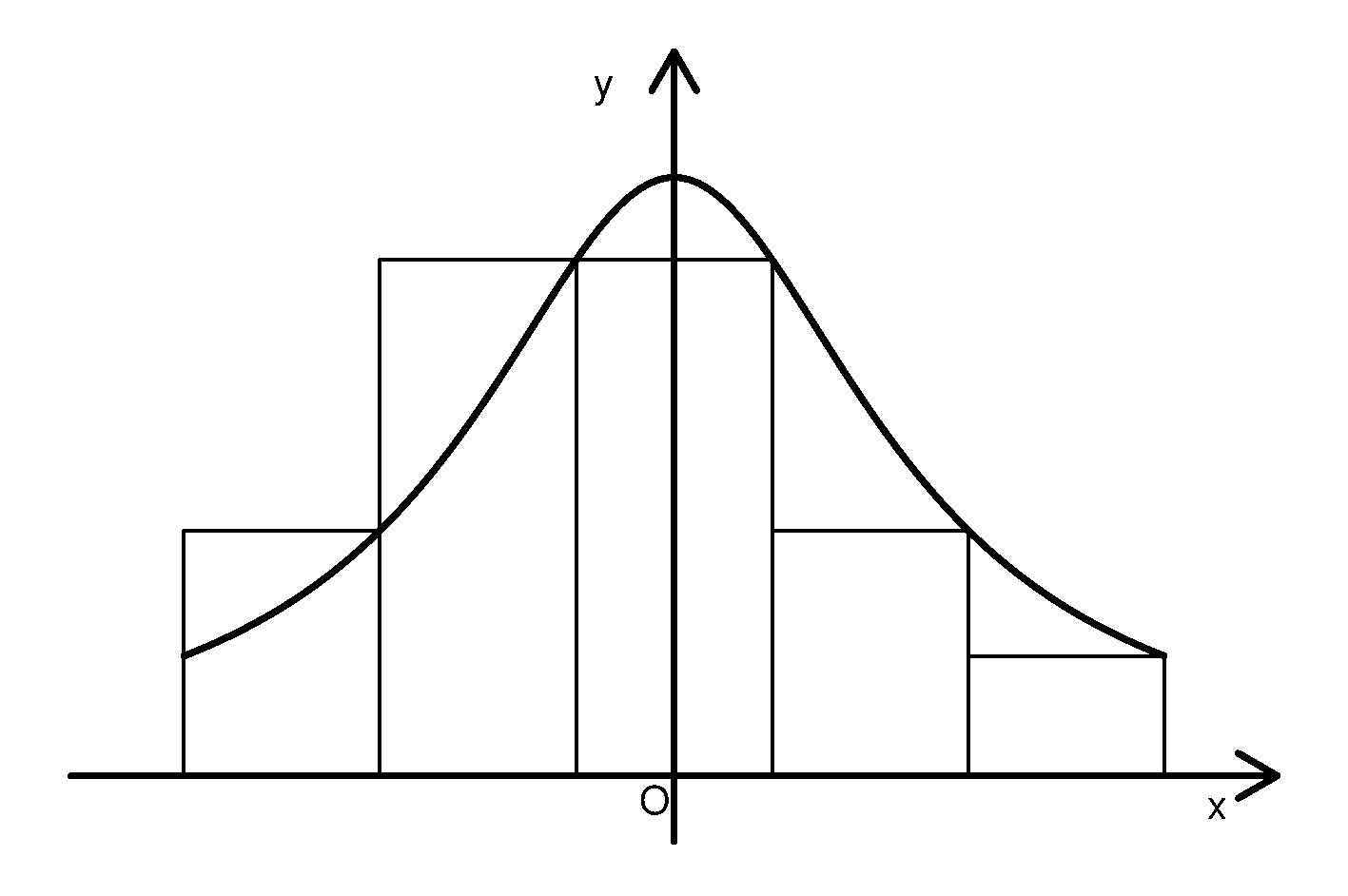
二、数值积分的基本概念
数值积分是定积分的数值近似计算方法。定积分是数学中一种重要的积分形式，它表示的是函数在某个区间上的累积效应。数值积分通过将定积分的区间分割成若干个子区间，然后在每个子区间上用近似的方法计算积分的值，最后将所有子区间的结果相加得到定积分的近似值。
三、数值积分的方法
四、数值积分的应用
数值积分在科学计算和工程领域有着广泛的应用。例如，在物理学中，可以用来计算物体的质量、能量等物理量；在经济学中，可以用来计算投资回报率、成本效益等经济指标；在工程学中，可以用来求解复杂的力学问题、热传导问题等。此外，数值积分还可以用于计算机图形学、信号处理等领域。
五、结论
数值积分是一种重要的数学方法，它在科学计算和工程领域有着广泛的应用。本文介绍了数值积分的基本概念、方法和应用，希望能帮助读者更好地理解和应用数值积分。同时，随着计算机技术的不断发展，数值积分的精度和效率也在不断提高，相信未来数值积分的应用将会更加广泛和深入。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
