夹逼定理
标题:夹逼定理
夹逼定理是数学中一种非常重要的证明方法,其思想主要是通过在某个特定区间内的数序列进行操作,来得出该区间内某函数的极限值。这种定理在实数集的函数分析中有着广泛的应用,本文将介绍夹逼定理的原理和实际应用。
一、夹逼定理的原理
夹逼定理主要描述的是在实数集中,如果存在两个数序列,且这两个数序列都满足一定的条件,那么它们之间的所有数也满足相同的条件。具体来说,假设我们有一个函数f(x)在某个区间内定义,且这个函数在某个点x0处的极限存在,那么我们可以通过构造两个数序列来逼近这个极限值。这两个数序列分别是单调递增和单调递减的,并且它们都满足f(x)的取值范围,且最终两个序列的值将逼近同一个值,这就是我们要求的极限值。
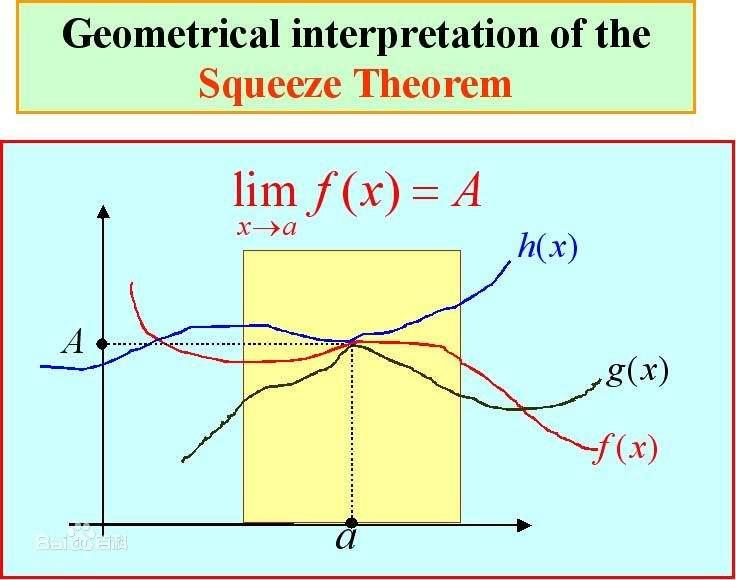
二、夹逼定理的应用
夹逼定理的应用非常广泛,其中最常见的就是用于求极限。在求解一些复杂的数学问题时,我们往往无法直接得出答案,而是需要通过一些方法来逼近答案。这时,夹逼定理就派上了用场。例如,在求解某些数列的极限时,我们可以通过构造两个收敛于同一值的单调数列来逼近该数列的极限值。此外,在实数集的函数分析中,夹逼定理也被广泛应用于求解一些函数的极限值。
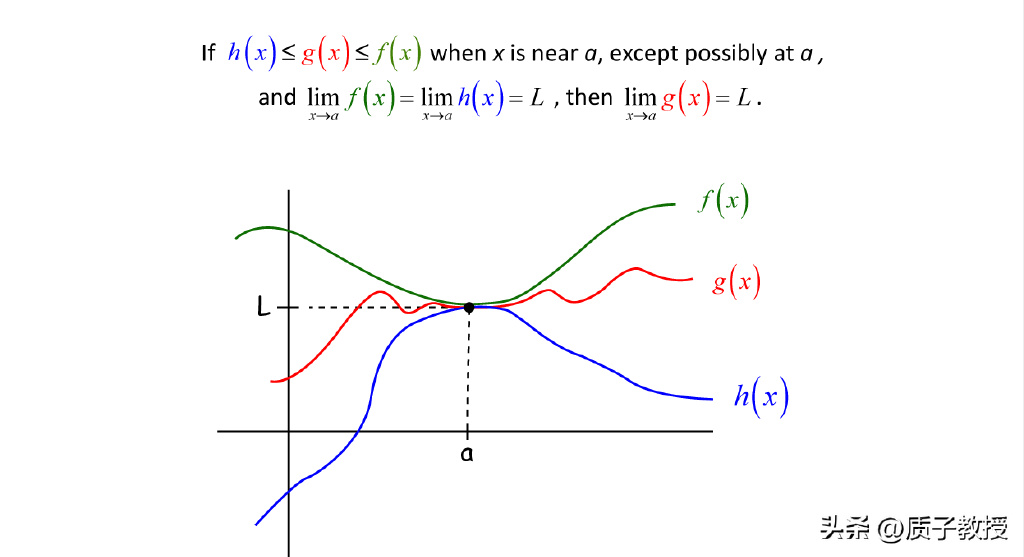
三、实例分析
以一个具体的例子来说明夹逼定理的应用。假设我们要求解数列1/n的极限值(n趋向于无穷大)。我们可以构造一个上界数列和下界数列,比如上界为2/n,下界为1/(n+1)。这两个数列都随着n的增大而趋向于0,因此我们可以认为这两个数列所夹的区间内的所有数(即1/n)也趋向于0。这就是通过夹逼定理求解数列极限的一个典型例子。
四、总结
夹逼定理是数学中一个非常重要的证明方法,它可以帮助我们求解一些复杂的数学问题。通过构造两个单调数序列来逼近某个函数或数列的极限值,我们可以得到非常精确的结果。在实际应用中,夹逼定理也被广泛应用于各个领域。对于学习数学的人来说,掌握夹逼定理的原理和应用方法是非常重要的。
希望以上内容能帮助你更好地理解夹逼定理。



















