文章标题：贝塔分布

在概率论与统计中，贝塔分布（Beta Distribution）是一种重要的概率分布。它在处理正实数数据以及某种条件下的小比例概率分布问题时特别有用。本文将介绍贝塔分布的定义、性质、应用场景以及其与其他分布的关系。

一、贝塔分布的定义

贝塔分布是一种连续概率分布，用于描述两个正实数参数的概率密度分布情况。具体地，若要衡量一组变量之间是否遵循一个共同的率或者比率关系时，常常用贝塔分布作为辅助模型进行评估。它的形式如下：

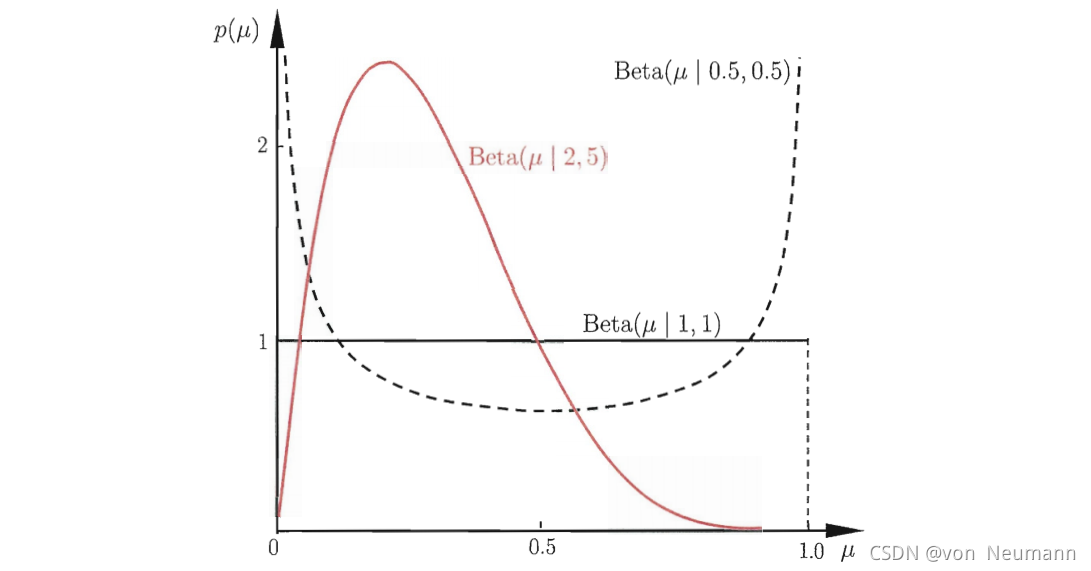
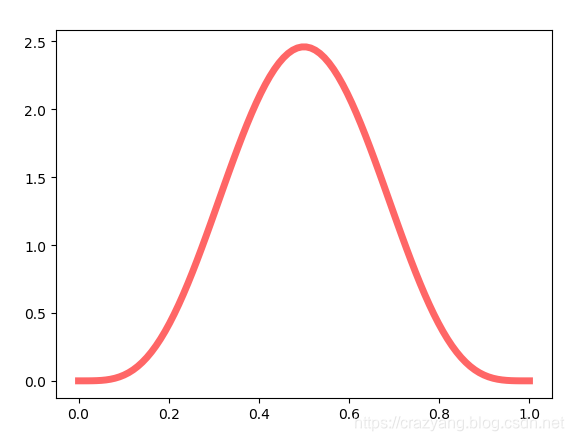
![图：贝塔分布图示]

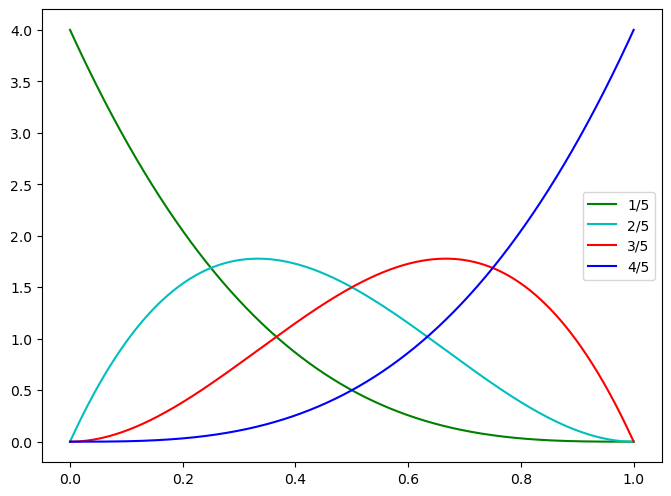
[注意：此处应插入一张贝塔分布的图形，以帮助读者更好地理解其形态和特点。]

二、贝塔分布的性质

贝塔分布具有以下性质：

1. 参数：贝塔分布有两个正实数参数，通常表示为α和β。这两个参数决定了分布的形状和位置。
2. 范围：贝塔分布的取值范围在0到1之间，因此它特别适合描述比例或比率数据。
3. 形状变化：随着参数α和β的增加或减少，贝塔分布的形状也会发生相应变化。当α或β增加时，密度曲线更加偏向中心。反之，则偏向两翼。
4. 应用领域：在生物学、社会科学和经济分析等多个领域都有广泛应用。如金融投资时对于概率预测等场合会频繁用到该模型进行参数估计。

三、应用场景及实例分析

（以下以“食品口味选择调查”为示例）在食品市场调研中，我们可以利用贝塔分布来描述消费者对不同口味食品的偏好程度。通过收集不同年龄、性别等群体对某种食品口味的偏好数据，然后根据这些数据利用贝塔分布进行分析，以估计各类口味的消费者占比以及它们之间的关系等。这种分析对于生产厂家设计新的食品产品有着非常重要的参考价值。

四、与其它分布的关系

贝塔分布在某些特定情况下可以与其他概率分布相互转换。例如，当两个参数α和β都很大时，贝塔分布可以近似为正态分布；在特定的条件下，它也可以与狄利克雷分布等其它复杂概率分布相互转换。这表明贝塔分布在概率论与统计中具有广泛的应用前景和重要的理论价值。

五、总结

本文介绍了贝塔分布的定义、性质、应用场景以及与其他分布的关系。通过学习这一知识，读者能够更深入地了解正实数数据及小比例概率的测量方法与实际应用情况。此外，掌握了贝塔分布也能更好地解决很多与统计和数据相关的实际问题，包括但在不限于分析人的消费行为习惯和消费需求等领域中的决策制定。随着对这种统计方法了解的加深，读者能够利用这一模型去描述更多场景的变量之间比率或关系变化规律等现实问题，有助于进行精准预测与数据分析处理等实际操作任务。希望本篇文章能够帮助大家对贝塔分布有更全面的理解。