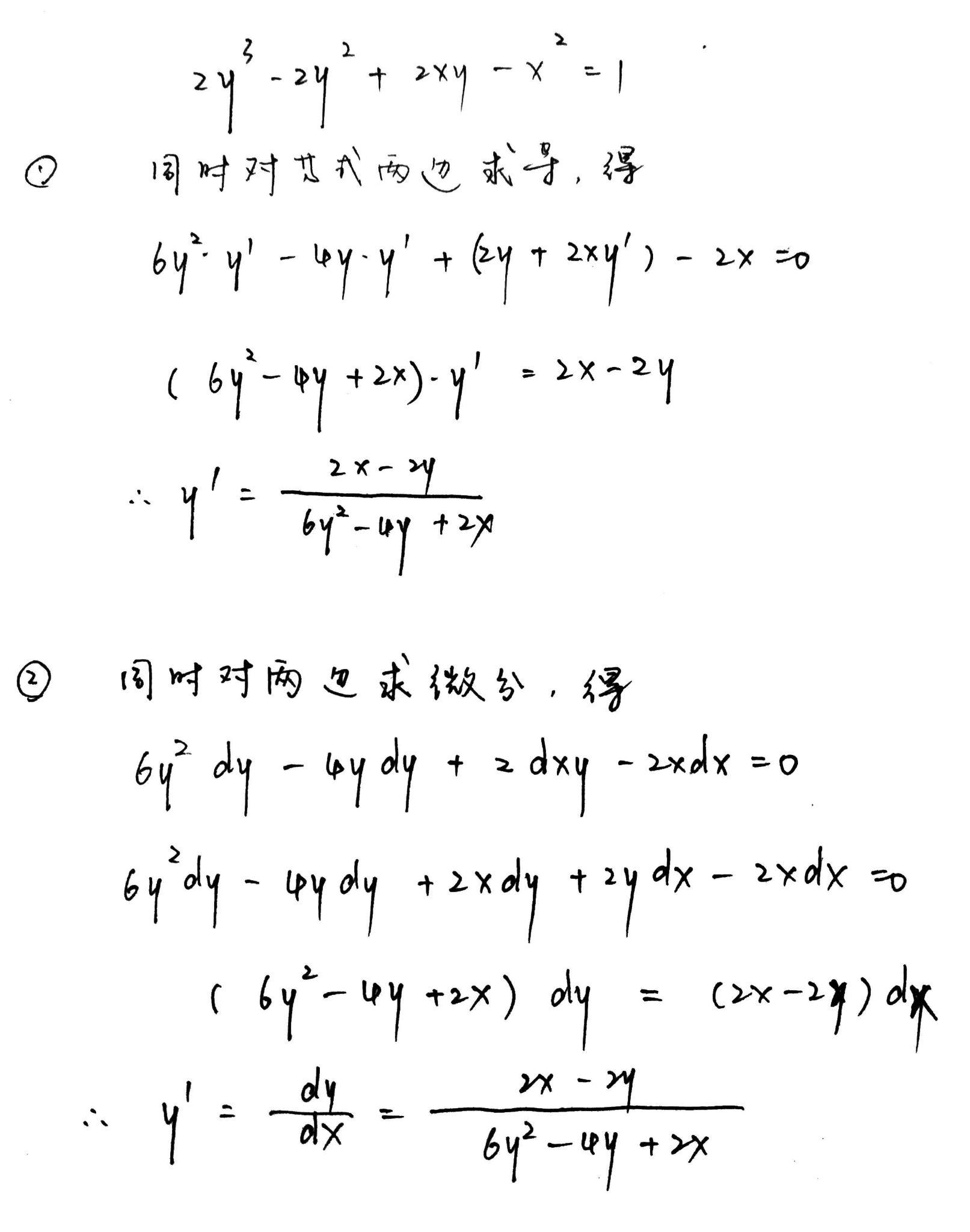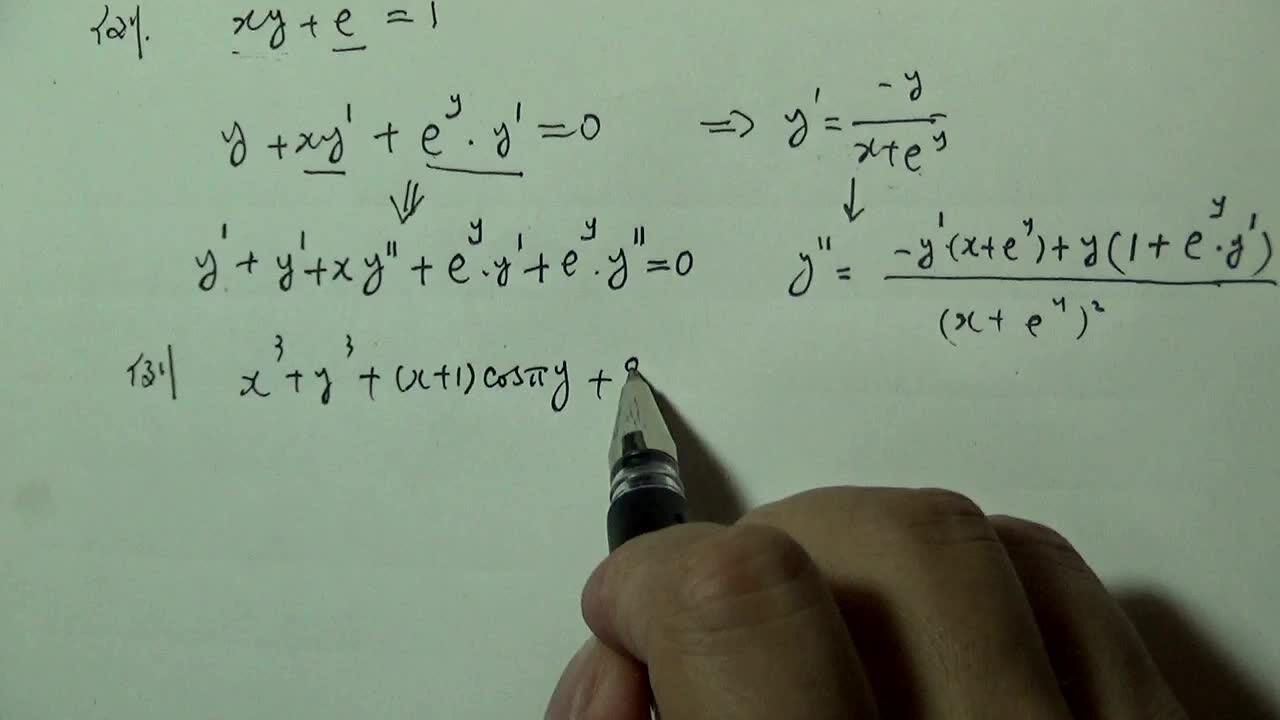文章标题:隐函数求导公式
引言:
在数学领域中,导数是用于表示函数局部变化的重要概念。当面对未知的函数关系时,我们常常需要使用隐函数求导公式来求解其导数。本文将详细介绍隐函数求导公式的概念、应用及注意事项。

一、隐函数求导公式概念
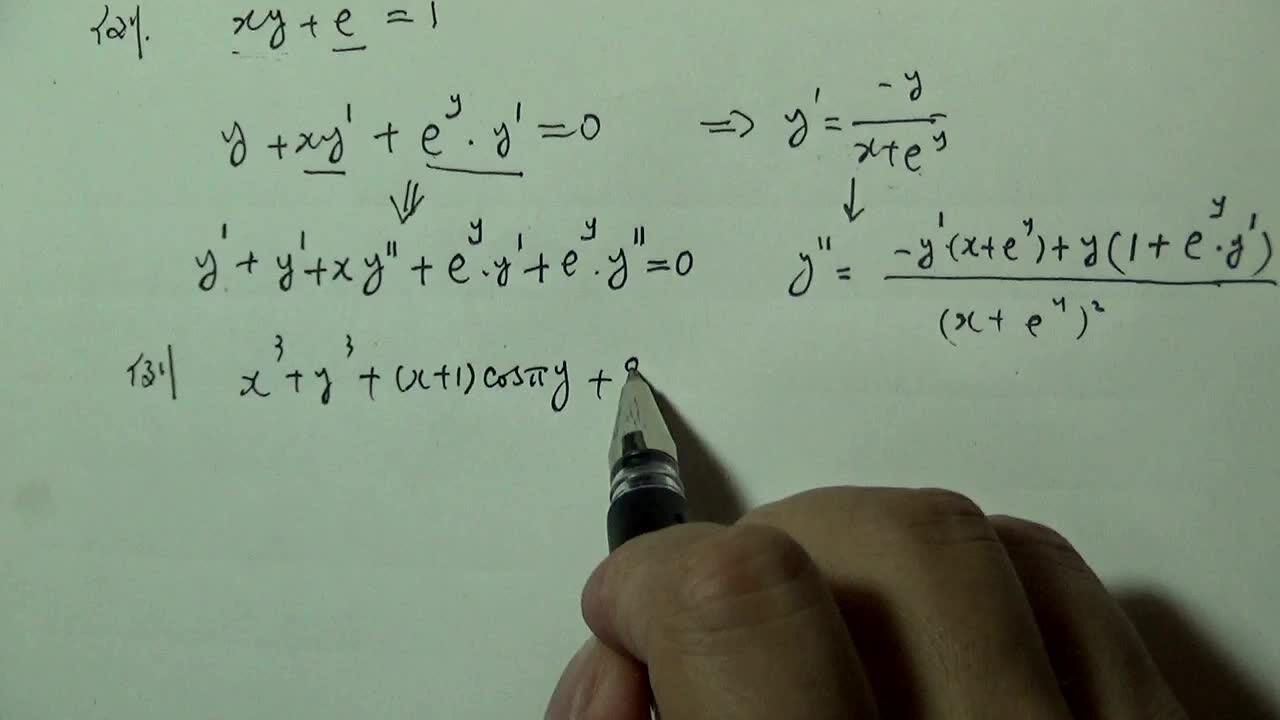
隐函数求导公式,是一种通过已知条件(如函数的约束关系)来推导未知函数(如某个函数的因变量与自变量之间的关系)的导数的方法。这种求导方式在处理一些复杂的数学问题时显得尤为重要。
二、隐函数求导公式的应用
- 确定函数的单调性:通过隐函数求导公式,我们可以得到函数的导数,从而判断函数的单调性。
- 解决最优化问题:在许多实际问题中,我们常常需要找到某个函数的最优解。这时,我们可以通过隐函数求导公式找到函数的极值点,从而确定最优解。
- 求解物理问题:在物理学中,许多问题都可以转化为求解隐函数的问题。通过隐函数求导公式,我们可以轻松地解决这些问题。
三、隐函数求导公式的使用注意事项
- 确定因变量和自变量:在使用隐函数求导公式时,首先需要确定因变量和自变量。一般来说,因变量是我们想要研究的变量,而自变量则是影响因变量的其他变量。
- 理解约束条件:在使用隐函数求导公式时,需要理解并正确应用约束条件。这些约束条件是求解问题的关键。
- 掌握求导规则:在应用隐函数求导公式时,需要熟练掌握各种求导规则和技巧。只有掌握了这些技巧,才能更准确地求解问题。
四、结论
隐函数求导公式是一种非常有用的数学工具,它可以帮助我们更好地理解和研究函数的性质。在解决实际问题时,我们需要灵活运用隐函数求导公式,同时注意约束条件和求导规则的掌握。只有这样,我们才能更准确地求解问题并得出满意的答案。
五、补充内容:常见隐函数求导的实例分析
- 参数方程求导:在某些问题中,我们需要根据参数方程来求解隐函数的导数。例如,通过极坐标系下的曲线方程来求解该曲线的切线斜率。此时可以使用链式法则等求导规则进行求解。
- 多变量隐函数的处理:当涉及到的函数为多变量时,隐函数的求导需要借助多元微积分的知识来处理。比如需要掌握多元函数的偏导数和全微分等概念及计算方法。
以上就是关于隐函数求导公式的介绍及应用示例。在实际学习和应用中,我们还需要不断地深入研究和练习才能熟练掌握这个工具。