一、线性拟合的概述
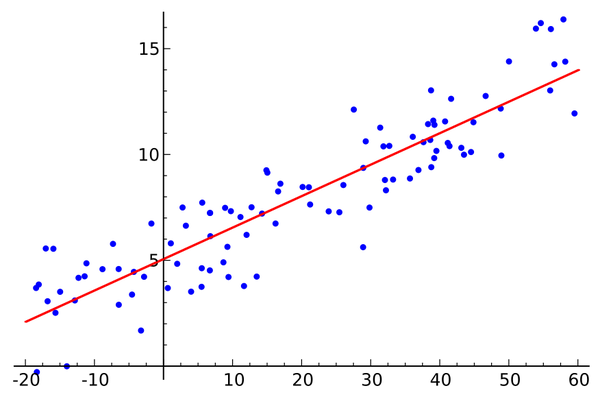
线性拟合是一种数学方法,用于通过一组数据点来寻找一条最佳的直线或曲线。在现实生活中,线性拟合被广泛应用于各种领域,如统计学、物理学、经济学等。通过线性拟合,我们可以更好地理解数据之间的关系,预测未来的趋势,以及进行其他数据分析。
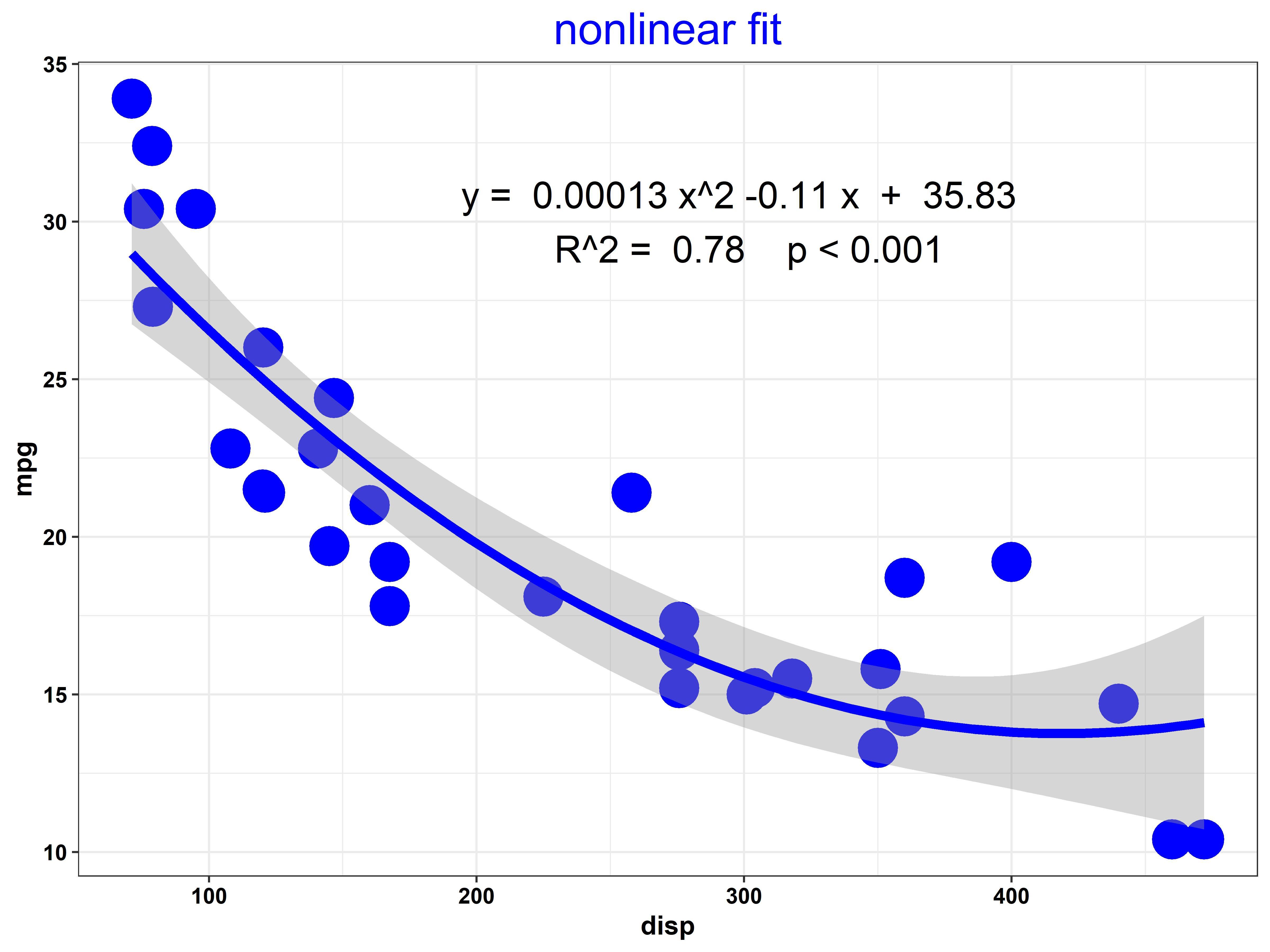
二、线性拟合的基本原理
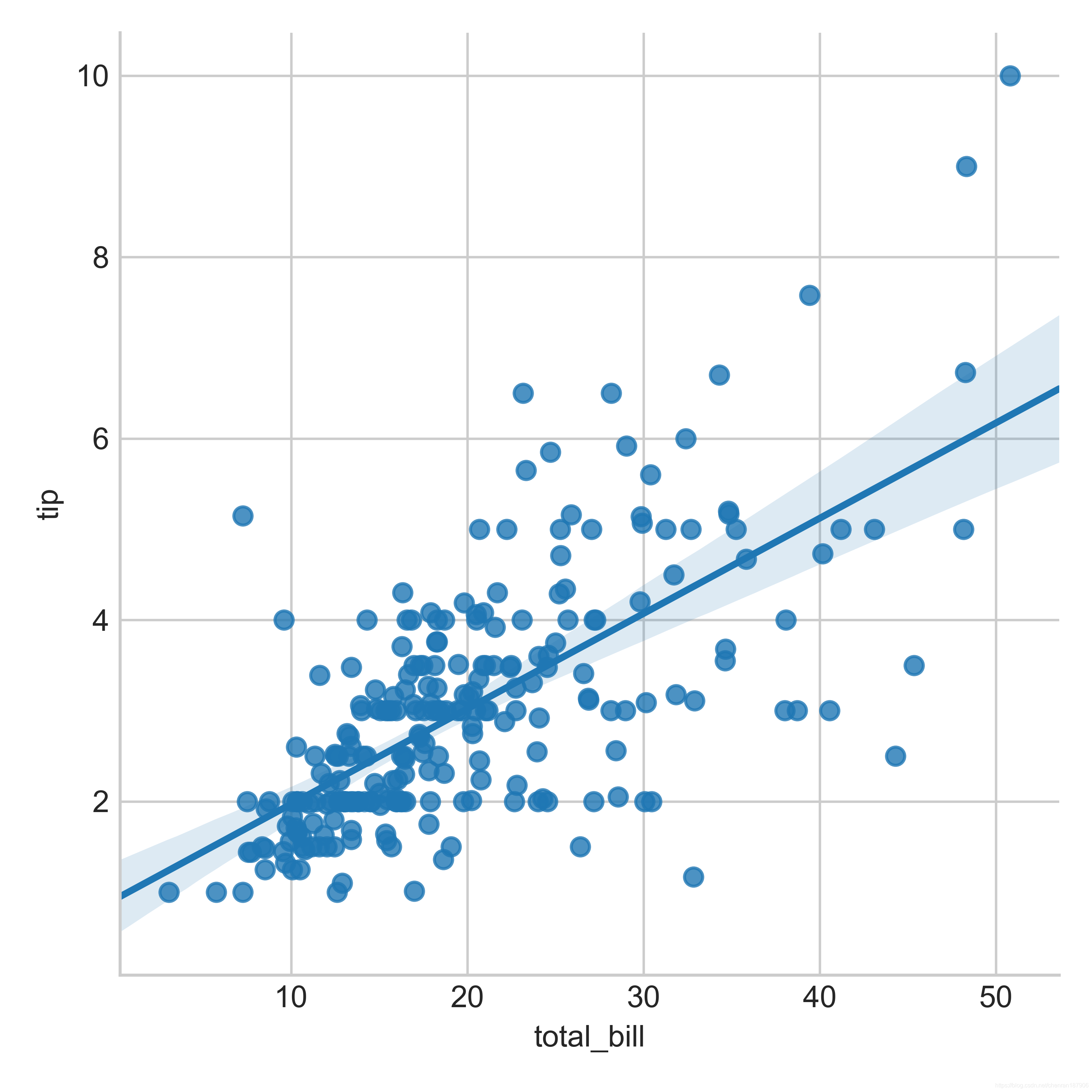
线性拟合的基本原理是通过最小化预测值与实际值之间的误差来寻找最佳的拟合线。具体来说,我们使用一组数据点的坐标,通过计算每个数据点到拟合线的垂直距离的平方和,来找到使这个和最小的拟合线。这条拟合线就是最能反映数据点之间关系的直线或曲线。
三、线性拟合的步骤
- 数据准备:首先,我们需要收集一组数据,包括自变量和因变量。这些数据应该尽可能地反映我们想要研究的问题或现象。
- 建立模型:根据数据的性质和关系,建立适当的线性模型。这个模型应该能够反映自变量和因变量之间的关系,并且能够通过线性拟合来优化。
- 进行拟合:使用适当的算法和方法,将数据点代入模型中,寻找最佳的拟合线。这个过程通常需要使用计算机或编程软件来完成。
- 评估拟合效果:对得到的拟合线进行评估,检查其是否能够很好地反映数据点之间的关系。这可以通过计算误差、决定系数等统计量来完成。
- 应用结果:根据得到的拟合线,我们可以进行各种分析和预测。例如,我们可以根据自变量的值来预测因变量的值,或者研究自变量和因变量之间的关系等。
四、总结
线性拟合是一种重要的数据分析方法,它可以帮助我们更好地理解数据之间的关系,预测未来的趋势,以及进行其他数据分析。通过掌握线性拟合的基本原理和步骤,我们可以更好地应用它来解决实际问题。同时,我们也需要注意选择适当的模型和方法,以及正确地评估拟合效果,以确保得到的结果可靠和有效。






















