文章标题：双精度浮点型
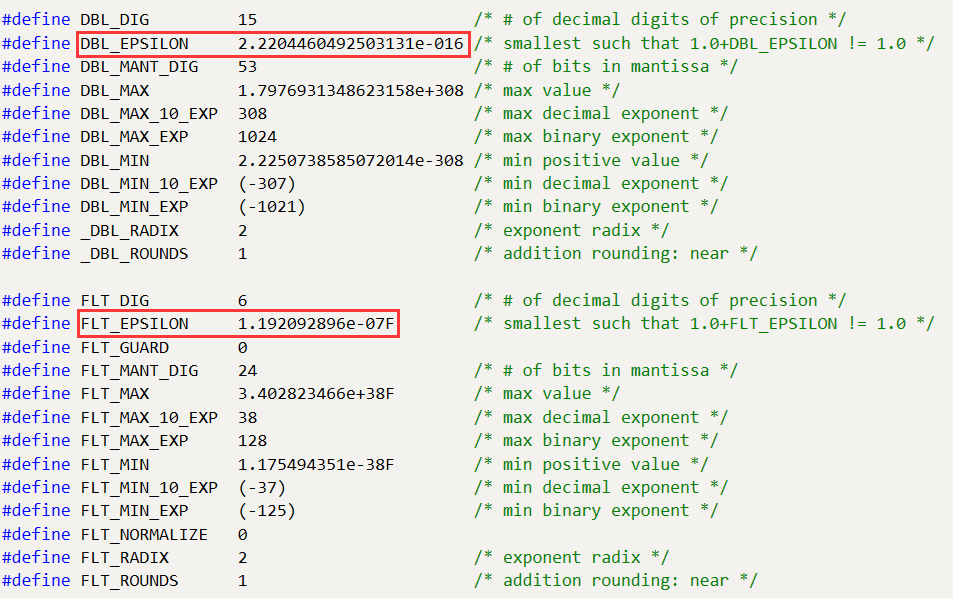
在计算机科学中，双精度浮点型（Double Precision Floating Point）是一种重要的数据类型，它被广泛应用于各种科学计算和数值计算中。本文将介绍双精度浮点型的基本概念、原理、应用以及与其他数据类型的比较。
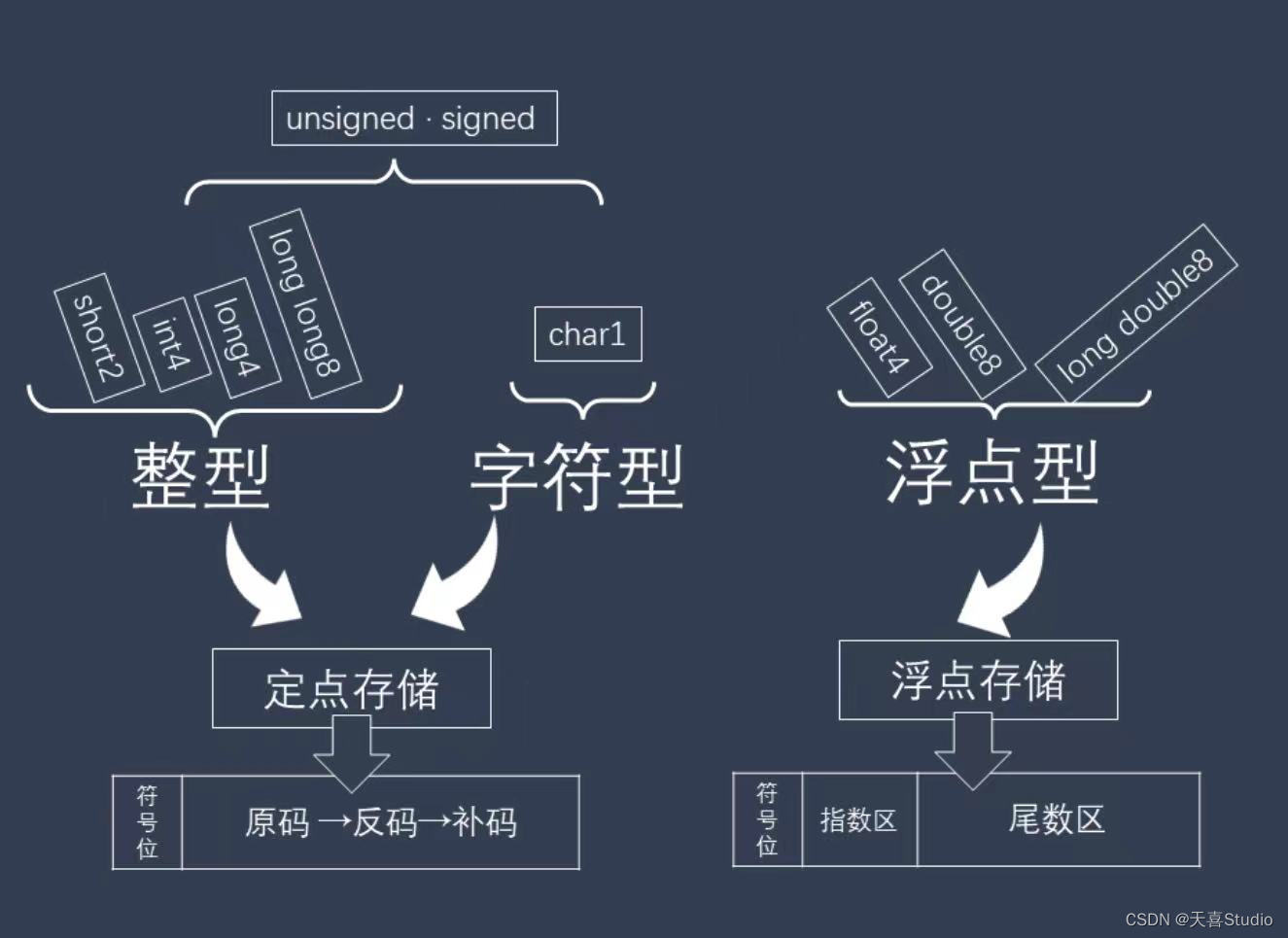
一、双精度浮点型的基本概念
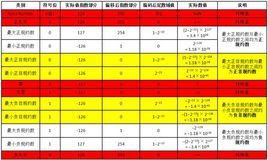
双精度浮点型是一种在计算机中表示实数的方法，它通过将实数分解为符号位、指数位和尾数位三部分来表示和存储。双精度表示可以表示一个较大的范围的值，且能以相对高的精度来表示实数。相比于单精度浮点型（Single Precision Floating Point），双精度能够表示更大的数、更小的数以及更高的精度。
二、双精度浮点型的原理
双精度浮点型的原理主要基于IEEE 754标准，该标准定义了浮点数的表示方法。在双精度浮点型中，一个数由三部分组成：符号位（S）、指数位（E）和尾数位（M）。符号位用来表示数的正负，指数位用来表示数的数量级，尾数位则用来表示数的具体值。通过这三部分的组合，计算机可以精确地表示和计算实数。
三、双精度浮点型的应用
双精度浮点型在科学计算和数值计算中有着广泛的应用。例如，在物理、化学、工程等领域中，需要进行大量的数值计算和模拟，这些计算往往需要高精度的数据表示和计算能力。此外，在图像处理、音频处理、金融计算等领域，也需要使用双精度浮点型来保证数据的准确性和可靠性。
四、与其他数据类型的比较
与整数型等其他数据类型相比，双精度浮点型具有更高的精度和更大的范围。然而，由于它需要更多的存储空间和计算资源，因此在某些情况下可能会影响程序的性能。因此，在选择使用双精度浮点型时，需要根据具体的应用场景和需求进行权衡。
五、结论
双精度浮点型是一种重要的数据类型，它具有高精度和大范围的特点，被广泛应用于各种科学计算和数值计算中。虽然它需要更多的存储空间和计算资源，但在许多情况下，这种牺牲是值得的，因为它可以保证数据的准确性和可靠性。随着计算机技术的不断发展，双精度浮点型将继续在各种应用中发挥重要作用。
以上就是关于双精度浮点型的介绍，希望对大家有所帮助。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
