向量的定义
一、向量的定义
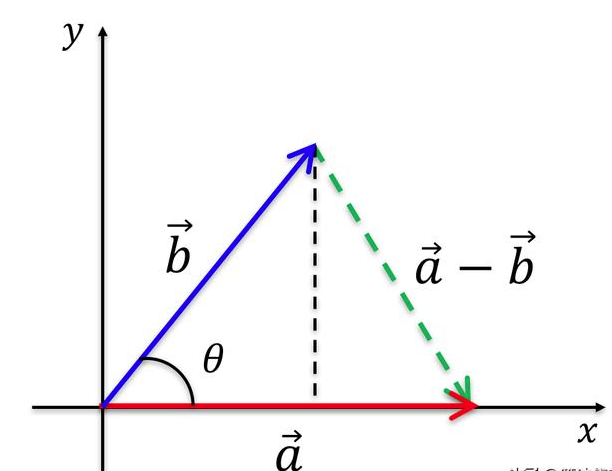
在数学中,向量是一个非常基础且重要的概念。那么,究竟什么是向量呢?下面我们将对向量进行详细的定义和解释。

一、向量的概念
向量是一种带有方向和大小的几何对象。它不仅仅是一个长度或一个数轴上的点,它是一个能够同时描述方向和大小的物理量。在数学和物理中,向量常被用来描述物理现象中的大小和方向,如速度、力等。
二、向量的表示
向量通常用大写字母表示,如向量A、向量B等。向量的方向通常用箭头表示,而大小则由向量的模长来决定。此外,我们还可以用坐标来表示向量,如二维平面上的向量可以表示为(x, y)的形式。
三、向量的基本性质
- 自由性:向量具有自由性,即可以在空间中自由移动而不改变其大小和方向。
- 模长:向量的模长是描述其大小的一个量,对于二维向量(x, y),其模长可以定义为|a|=√(x²+y²)。
- 加减运算:同向量的加减可以通过对其分量进行相应的加减来实现。例如,有两个同类型的向量A和B,A与B的加减可以通过各分量的对应相加或相减来得出新的向量结果。
- 线性组合:在平面或空间中,可以由多个向量进行线性组合得到新的向量。这种组合可以理解为通过改变各个向量的长度和方向来生成新的向量。
四、向量的应用
向量在数学、物理、工程等领域都有广泛的应用。例如,在物理学中,我们可以使用向量来描述物体的速度、加速度等;在工程中,我们可以使用向量来描述信号的强度和方向等。同时,由于计算机的发展,我们可以将许多基于向量的计算算法转化为高效的算法进行实现,使得计算更为便捷。
综上所述,向量是描述物体的大小和方向的一种工具,其表示形式和计算方法对于学习和理解数学中的其他概念具有重要的意义。在日常生活和科研中,我们需要更多地掌握和应用这一基础工具,从而更好地解决各种实际问题。



















