双线性插值
双线性插值（Bilinear Interpolation）是一种在图像处理和计算机图形学中常用的技术，用于提高图像的分辨率或对图像进行平滑处理。在许多情况下，我们可能需要将一个低分辨率的图像或一个不清晰的图像进行放大或改善其质量，这时双线性插值就可以发挥其作用。
一、基本概念
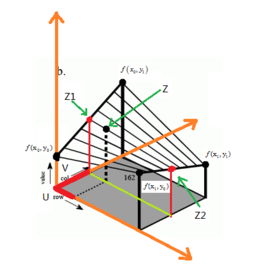
双线性插值是一种基于线性插值的扩展。在二维空间中，通过已知的四个点的值来估算目标点的值。与传统的插值方法相比，双线性插值在两个维度上分别进行一次线性插值，得到的结果更加准确且平滑。
二、工作原理
确定目标像素位置：首先确定目标像素在原图像中的位置。
线性插值：基于水平方向（x轴）和垂直方向（y轴）上两个点的颜色值，计算在这两个方向上的插值。对于水平方向的线性插值，可以计算在一条线上所有x值的加权平均值，垂直方向同理。
组合插值结果：将水平和垂直方向的插值结果再次进行一次插值，得到目标像素的最终颜色值。
三、应用场景
图像缩放：当需要将一个低分辨率的图像转换为高分辨率的图像时，可以通过双线性插值技术实现这一目标。双线性插值可以根据邻近的像素信息计算出目标像素的颜色值，从而使放大后的图像看起来更加自然清晰。
计算机图形学：在三维图形渲染中，当从低分辨率纹理贴图映射到高分辨率表面时，也需要使用双线性插值来保证图像的质量。
四、总结
双线性插值是一种在图像处理和计算机图形学中非常实用的技术。它能够根据已知的四个点的信息，精确地估算出目标点的颜色值或其它属性值。通过这种方法，我们可以有效地提高图像的分辨率和清晰度，使图像看起来更加自然和真实。同时，双线性插值算法简单且易于实现，因此被广泛应用于各种图像处理和计算机图形学应用中。
以上就是关于双线性插值的介绍和基本原理，希望对大家有所帮助。在实际应用中，我们还需要根据具体的需求和场景来选择合适的插值算法和技术。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
