一、完全二叉树的定义
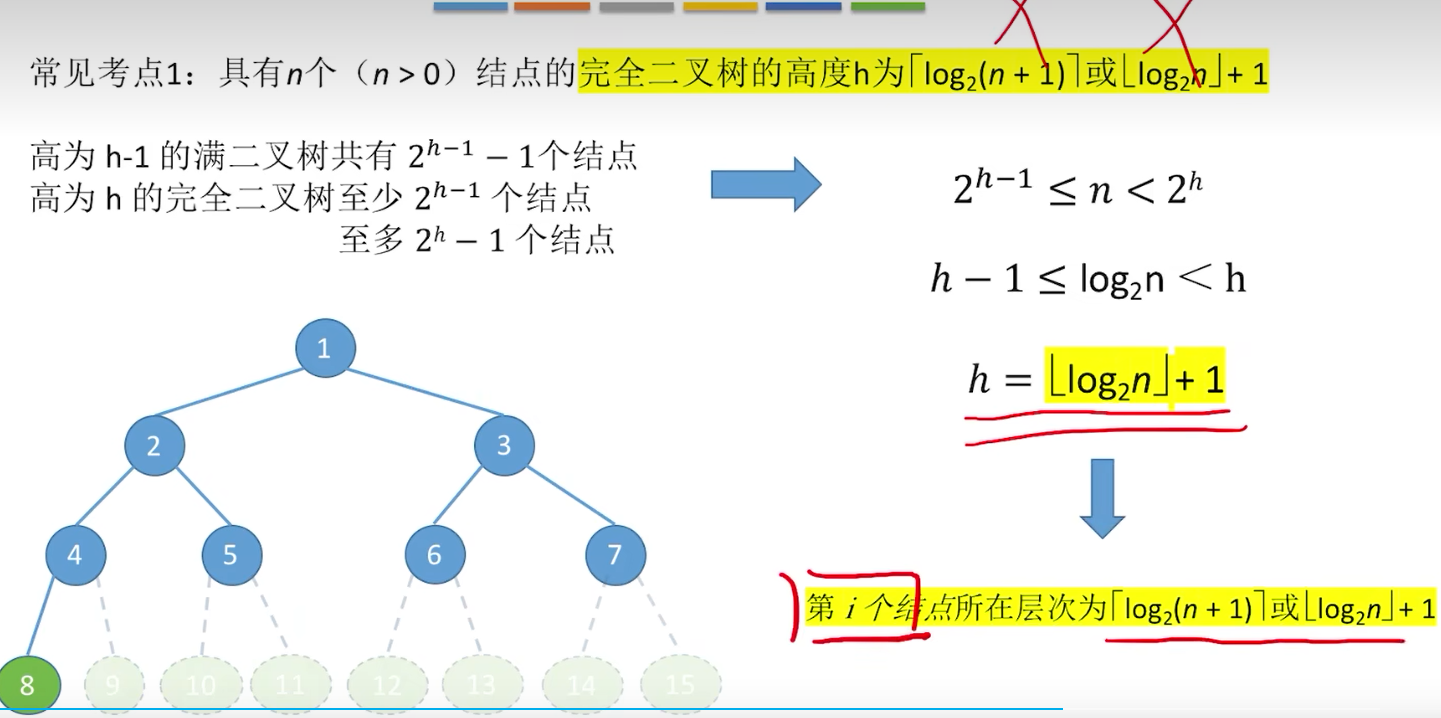
在计算机科学中，二叉树是一种常见的树形结构，完全二叉树则是二叉树的一种特殊形态。它不仅具备二叉树的基本性质，还有着独特的结构和特点。
1. 二叉树的基本概念
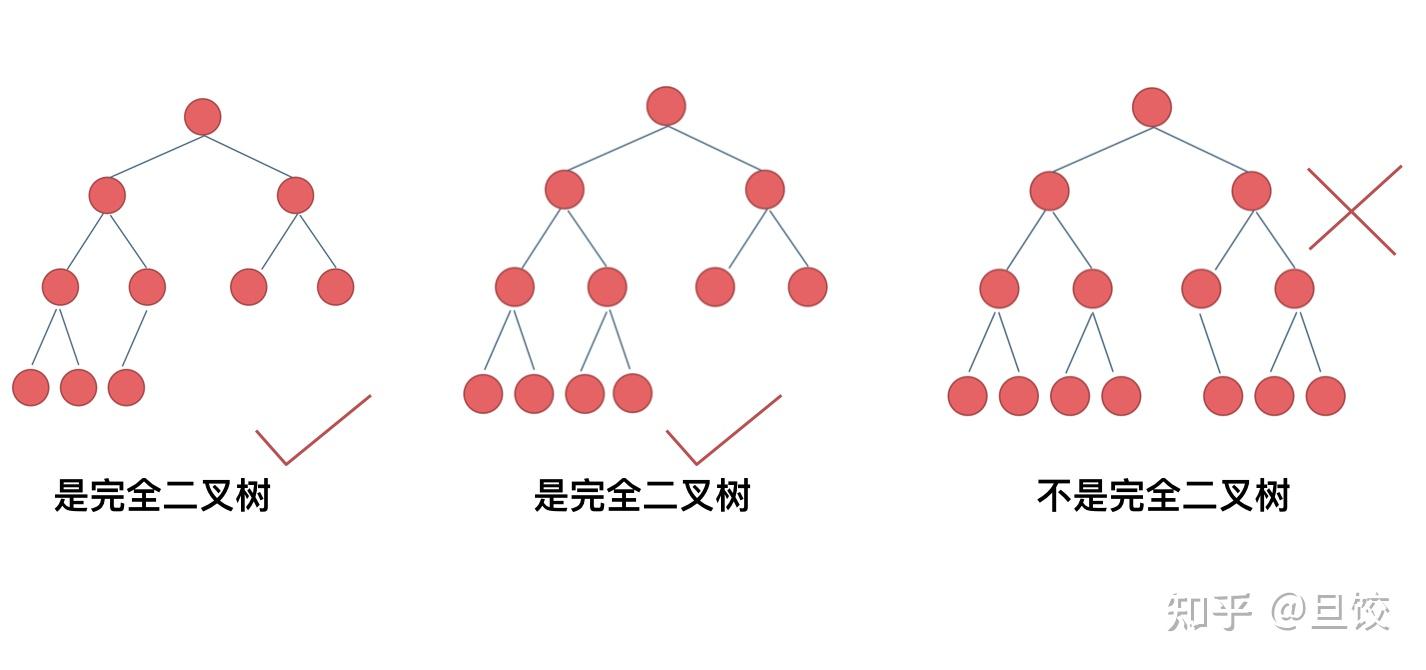
二叉树是一种每个节点最多有两个子节点的树结构，通常子节点被称作“左子节点”和“右子节点”。二叉树的递归结构使得其具有丰富的应用场景，如表达式树的构建、深度优先搜索等。
2. 完全二叉树的定义
完全二叉树是对普通二叉树的一种限制性规定，它的特点可以总结为以下三点：
（1）在完全二叉树的叶子节点中，所有节点的编号是连续的，不会出现中断的情况。也就是说，在任何一个层次上，都只有一个节点的位置被空缺或者遗漏。
（2）在完全二叉树的任何层中，最多只有右边的那部分叶子节点是不完全填满的。但总体来说，这不会影响到完全二叉树的性能和用途。
（3）在层次上，除了叶子节点以外，每一个有子节点的内部节点都是从左到右填充的。这就保证了从根节点到叶子节点的任何路径都是最大化的。
3. 完全二叉树的存储结构
完全二叉树的存储通常使用数组或者链表的形式进行存储。对于采用数组存储的完全二叉树来说，它充分利用了数组空间连续的特性，大大节省了存储空间。在存储过程中，父节点的索引可以轻松推算出其子节点的索引，这种特性使得完全二叉树在遍历和搜索方面具有很高的效率。
4. 完全二叉树的应用
由于完全二叉树的特性，它在很多领域都有广泛的应用。例如，在数据库索引中，B+树就是一种典型的完全二叉树结构；在数据压缩领域，哈夫曼树也常常采用完全二叉树的形式进行构建；在图论中，完全二叉树也是深度优先搜索等算法的重要数据结构之一。
总之，完全二叉树作为一种特殊的树形结构，具有独特的性质和广泛的应用场景。掌握其定义和特性对于理解计算机科学中的相关算法和数据结构具有重要意义。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
