什么是实数集
文章标题:什么是实数集
文章内容:

在数学领域中,实数集是一个基本概念,它在很多领域都起着至关重要的作用。那么,什么是实数集呢?

一、实数集的定义
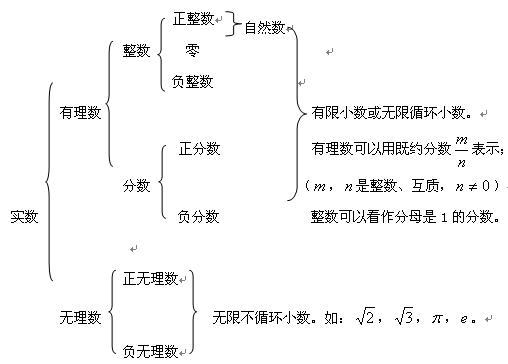
实数集,通常用大写字母R表示,是包括有理数和无理数的集合。有理数包括整数、正数、负数和分数等,而无理数则是不能表示为两个整数的比的数,例如π和e等。所有这些数构成了实数集。
二、实数集的性质
- 连续性:实数集具有连续性,即任意两个实数之间都可以找到其他实数。这是实数集与其他数集(如自然数集或整数集)的一个重要区别。
- 顺序性:实数集具有大小关系,可以比较任意两个实数的大小。同时,实数集也是一个有序集合,可以按照大小关系进行排列。
- 可数性:尽管实数集看起来很庞大,但它却是可数的。这意味着我们可以把实数一一对应地与自然数集进行配对。
三、实数集的应用
实数集在数学中有着广泛的应用。它是代数、几何、三角学和微积分等众多领域的基础。在现实生活中,实数集也被广泛应用在物理学、工程学、经济学和计算机科学等领域。例如,在物理学中,实数集被用来描述物理量的值;在计算机科学中,实数集则被用来表示各种数值数据。
四、总结
总之,实数集是数学中的一个基本概念,它包括了所有的有理数和无理数。它具有连续性、顺序性和可数性等重要性质,是数学和其他领域研究的基础。通过学习和理解实数集的概念和性质,我们可以更好地理解数学和其他领域中的许多问题。同时,实数集的应用也让我们认识到数学在现实生活中的重要性。因此,我们应该重视对实数集的学习和理解,为未来的学习和工作打下坚实的基础。



















