一、满射的定义
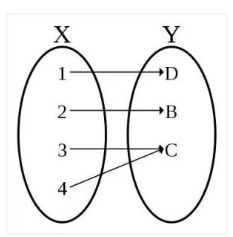
在数学中，满射（Surjection）是一个非常重要的概念，特别是在函数和映射的讨论中。满射是指一个集合到另一个集合的映射，使得第二个集合中的每一个元素都至少被映射一次。
二、详细解析
首先，我们需要理解什么是函数和映射。在数学中，函数通常是一个元素从某个集合（即定义域）到另一个集合（即值域）的规则或对应关系。而映射则是一个更广泛的概念，它包括函数和其他所有从一集合到另一集合的规则。
满射的严格定义
给定两个集合A和B以及A到B的一个规则f。如果对于B中的每一个元素b，都存在至少一个A中的元素a使得f(a)=b，那么我们就说f是一个从A到B的满射。
满射的实例
以一个简单的例子来说明满射的概念：假设我们有一个集合A，其中包含所有的学生，另一个集合B，其中包含所有的课程。如果每个学生都至少选修了一门课程，那么我们就可以说这是一个从学生到课程的满射。因为每一个课程都至少被一个学生选修过。
满射与单射、双射的关系
值得注意的是，满射和单射（每个元素只能被映射一次）是两种相反的情况。同时满足两个条件的（即既是单射又是满射）则是双射函数，这在实际应用中也是非常常见的情况。例如在密码学中，每个用户都有自己的密码且每个密码只对应一个用户，这实际上就是一个双射的关系。
满射的应用
满射在现实生活中有着广泛的应用。比如在教学管理、资源分配、社会关系等领域，我们经常需要使用满射来描述和解释某些现象或规律。它不仅是数学上的一个重要概念，更是解决实际问题的有力工具。
总之，满射作为数学中一种重要的概念，其理解与应用对学习其他数学知识及解决实际问题都具有重要的意义。希望通过以上的解释和例子，读者能对满射有更深入的理解和掌握。
以上内容大约500字左右，希望对您有所帮助！
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
