一、什么是抽样分布
抽样分布是一个重要的概念，广泛用于统计学领域，特别是概率论、回归分析以及决策分析中。当人们从一个更大的数据集或总体中选取样本时，这些样本的统计量（如均值、中位数、标准差等）会形成一个新的分布，这就是抽样分布。
二、抽样分布的详细解释
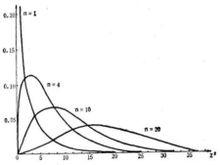
抽样分布描述的是从一个总体中随机抽取样本，样本大小不同，样本的统计量所形成的分布。这些统计量可以是任何基于样本数据的函数，如样本均值、样本方差等。在每次抽取新的样本时，都会产生一个新的小样本分布。而所有这些小样本分布的平均数和变化规律就构成了我们所说的抽样分布。
根据不同的统计量，我们可以将抽样分布分为不同的类型，如正态分布、t分布、F分布等。其中，正态分布是最常见的一种，当样本大小足够大时，样本均值的分布会接近正态分布。而t分布和F分布则是根据特定的情况和需要用于特定场景的抽样分布。
在统计学中，抽样分布的应用非常广泛。例如，在估计总体参数时，我们常常使用抽样分布来计算置信区间和置信水平。在回归分析中，我们使用抽样分布来估计回归模型的参数和预测值。在决策分析中，我们利用抽样分布来评估决策的准确性，如确定不同方案的成功概率等。
首先，每个样本的大小都对应着一个独特的抽样分布。其次，随着样本量的增加，抽样分布的形状和变化规律会逐渐接近于正态分布。最后，不同的抽样方法（如简单随机抽样、分层抽样等）会产生不同的抽样分布。
三、总结
总的来说，抽样分布是统计学中的一个重要概念，它描述了从总体中抽取的样本统计量的分布情况。通过了解和应用抽样分布，我们可以更好地理解数据的性质和变化规律，从而为后续的统计分析提供有力的支持。在现实生活和工作中，我们应该更加重视对抽样分布的学习和应用，以帮助我们更好地处理和分析数据。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
