文章标题:OLS回归

一、引言
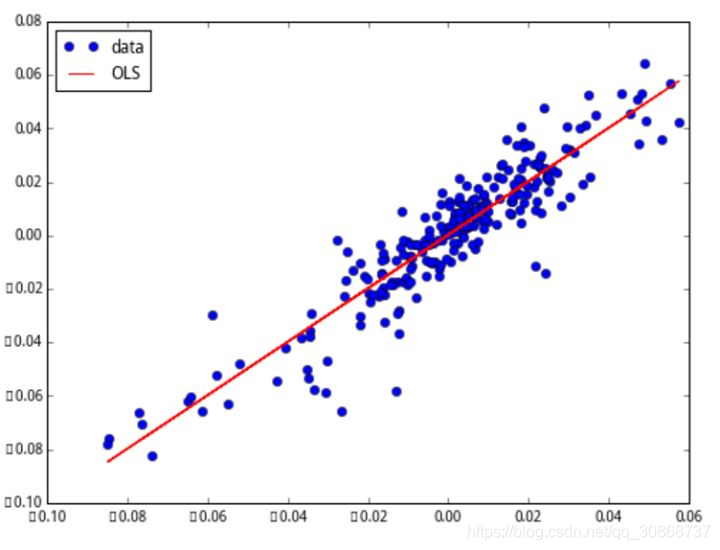
OLS回归,全称最小二乘法回归,是一种常见的统计模型。在数据分析、经济学、金融学等众多领域,都有着广泛的应用。它主要是为了建立两个或多个变量之间的线性关系模型,以便我们进行更深入的分析和预测。
二、OLS回归的基本概念
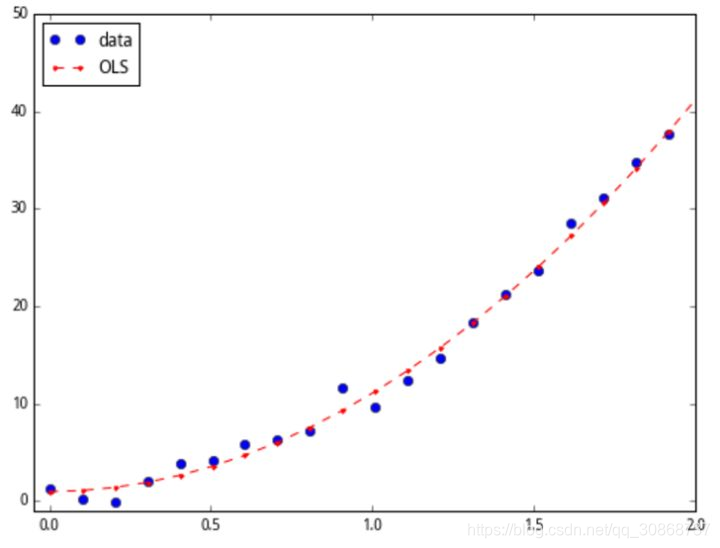
OLS回归的核心思想是寻找一条直线(或更高维度的平面),使得所有观测值到这条直线的垂直距离(即残差)的平方和最小。这样的一条直线,就称为最佳拟合直线。它以最小化误差的平方和为标准,求得最佳的函数匹配。
三、OLS回归的步骤
- 模型设定:根据数据的性质和关系,选择合适的变量,设定回归模型的形式。
- 数据收集:收集所需的数据,并进行清洗、整理,以满足模型的需求。
- 参数估计:利用最小二乘法,估计出回归模型的参数。
- 模型检验:对估计出的模型进行统计检验,看其是否符合预期的假设条件。
- 预测与决策:利用模型进行预测,并基于预测结果进行决策。
四、OLS回归的优点与缺点
优点:
- 简单易懂:OLS回归的原理和操作都比较简单,易于理解和掌握。
- 解释性强:回归模型可以清晰地解释变量之间的关系,以及自变量对因变量的影响程度。
- 预测效果好:在满足假设条件下,OLS回归的预测效果较好。
缺点:
- 对线性关系的假设:OLS回归假设变量之间存在线性关系,如果实际关系并非线性,则模型可能不准确。
- 对误差的假设:OLS回归假设误差服从正态分布,如果这个假设不成立,则模型的可靠性会受到影响。
- 多重共线性:如果自变量之间存在高度相关性,会导致参数估计不准确。
五、结论
总的来说,OLS回归是一种简单、有效的统计方法,广泛应用于各个领域。但是,在使用时需要注意其假设条件和限制,以确保模型的准确性和可靠性。同时,也需要根据实际情况选择合适的模型形式和变量,以得到更准确的结果。






















