文章标题：高斯求和公式
一、什么是高斯求和公式？
高斯求和公式，通常用于解决序列的快速求和问题，这个方法最早由高斯发现。在高斯研究中，高斯发现在将一列自然数逐一相加时，会有一些隐藏的规律可以被快速求得和，即可以通过数学公式迅速计算这些数字的和。这个方法对于孩子们在早期学习中学习序列的规律有着很大的帮助，也体现了数学的神奇魅力。
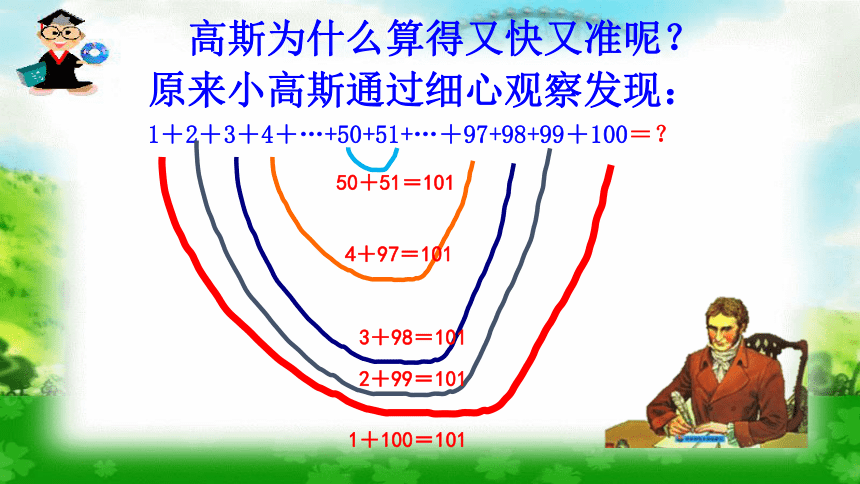
二、高斯求和公式的原理
高斯求和公式的原理主要基于等差数列的求和。对于一组等差数列，我们可以使用这个公式快速计算其和。其基本思想是将首项和末项相加，乘以项数的一半，即可得到总和。具体来说，对于等差数列a1, a2, a3, ..., an，其和S可以用以下公式表示：
S = n/2 * (a1 + an)
其中n为项数，a1为第一项，an为最后一项。
三、高斯求和公式的应用
高斯求和公式在数学中有着广泛的应用。除了在初等数学中用于解决简单的序列求和问题外，它还可以在更复杂的数学问题中发挥作用。例如，在物理学中，我们常常需要计算一系列数值的和来描述物体的运动状态或者能量分布。这时，高斯求和公式就能起到事半功倍的效果。
四、高斯求和公式的推广
除了基本的等差数列求和外，高斯求和公式还可以进行一些推广。例如，对于一些非等差数列的序列，我们可以通过一些变换将其转化为等差数列的形式，然后使用高斯求和公式进行计算。此外，对于一些更复杂的数学问题，我们还可以将高斯求和公式的思想进行拓展，以解决更复杂的问题。
五、总结
高斯求和公式是一个简单而强大的数学工具，它可以帮助我们快速解决序列的求和问题。掌握高斯求和公式的原理和应用，不仅可以在学习和生活中解决问题，还能帮助我们理解数学的魅力。我们应该不断探索数学世界中的奇妙规律，不断尝试使用各种方法和技巧来解决问题。只有这样，我们才能真正掌握数学的精髓。
以上就是关于高斯求和公式的介绍和应用。希望能够帮助大家更好地理解这个数学工具的原理和应用方法。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
