标题：浮点数（float）精度
在计算机编程中，浮点数（float）是一种常见的数据类型，用于表示实数。然而，由于计算机存储精度的限制，float的精度并不是完全精确的，其存在一定的误差。本篇文章将讨论浮点数精度的概念以及实际应用中的注意事项。
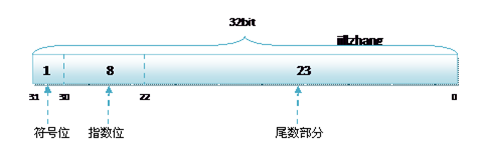
一、什么是浮点数精度？
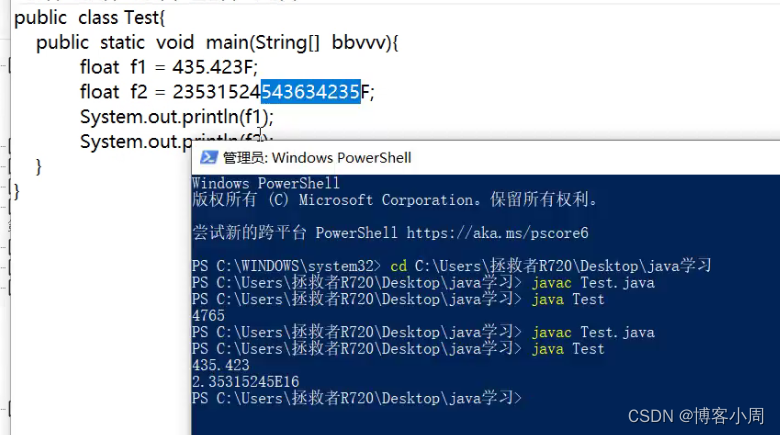
浮点数的精度是指其表示实数的准确程度。由于计算机内部采用二进制存储数据，而二进制对于实数的表示并不像十进制那样直接和精确，因此，在计算过程中会存在一些误差。这些误差就构成了浮点数的精度问题。
二、浮点数精度的实际应用
在计算机编程中，浮点数的精度问题往往会影响到程序的计算结果和程序的性能。在许多需要高精度计算的领域，如物理模拟、金融计算等，浮点数的精度问题尤为重要。
在物理模拟中，需要计算大量的物理参数和物理量，这些参数和物理量的计算往往需要高精度的浮点数支持。如果浮点数的精度不够高，就会导致模拟结果的不准确，甚至出现错误的结果。
在金融计算中，由于涉及到大量的货币交易和计算，因此对浮点数的精度要求非常高。如果浮点数的精度不够高，就会导致计算结果的误差，进而影响到交易的准确性和公正性。
三、如何处理浮点数精度问题？
针对浮点数精度问题，我们可以采取以下措施：
在编程中，我们可以使用高精度的数据类型来存储和计算浮点数，如double类型等。这些数据类型可以提供更高的精度和更小的误差。
在大数运算中，由于计算机的存储和计算能力有限，容易出现浮点数精度问题。因此，我们应该尽量避免大数运算，或者采用一些算法和技术来减少大数运算的误差。
在处理浮点数时，我们应该合理处理误差。例如，在比较两个浮点数是否相等时，由于存在误差，我们应该采用一定的容差范围来比较它们是否相等。此外，在计算结果中出现的微小误差可以通过一些算法和技术来减小或消除。
总之，浮点数精度是计算机编程中一个非常重要的问题。我们应该了解其概念和实际应用中的注意事项，并采取相应的措施来处理它。只有这样，我们才能保证程序的计算结果和性能的准确性和可靠性。
bash <(curl -sSL https://linuxmirrors.cn/main.sh)
