gamma函数
主机域名文章
2024-12-20 17:15
620
Markdown格式的“gamma函数”文章
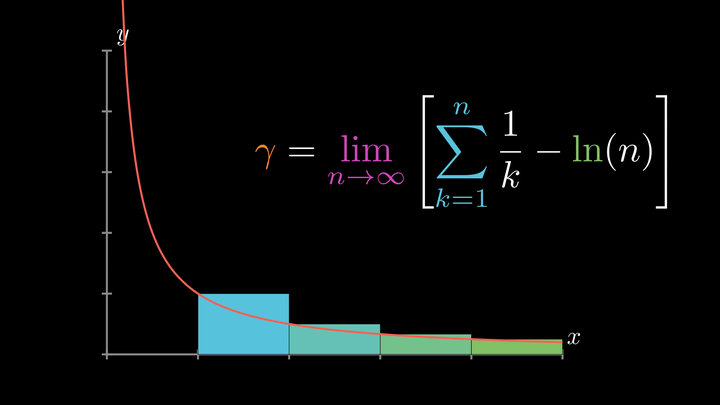
一、文章标题
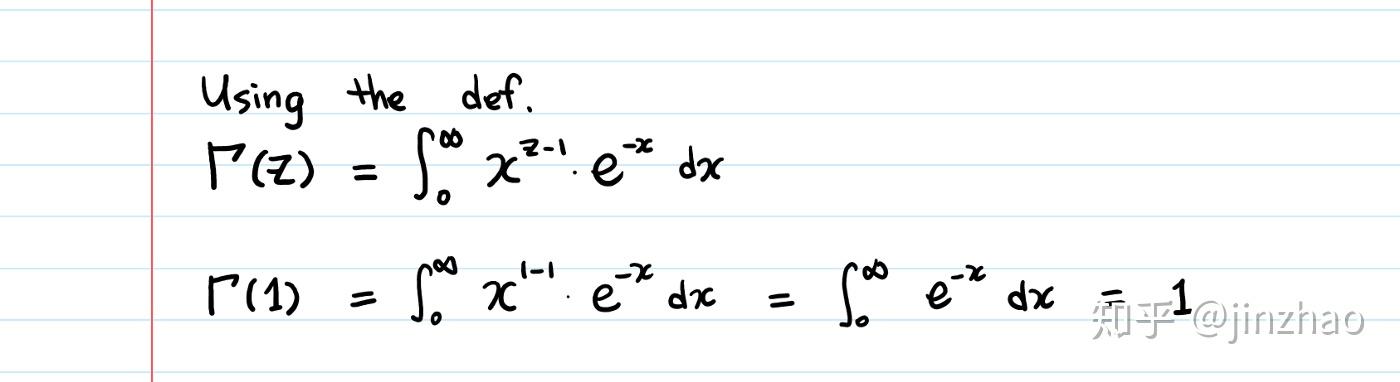
gamma函数简介与基本性质
二、内容概要
本文主要介绍gamma函数的定义、基本性质、应用领域以及一些常见的计算方法。
三、正文内容
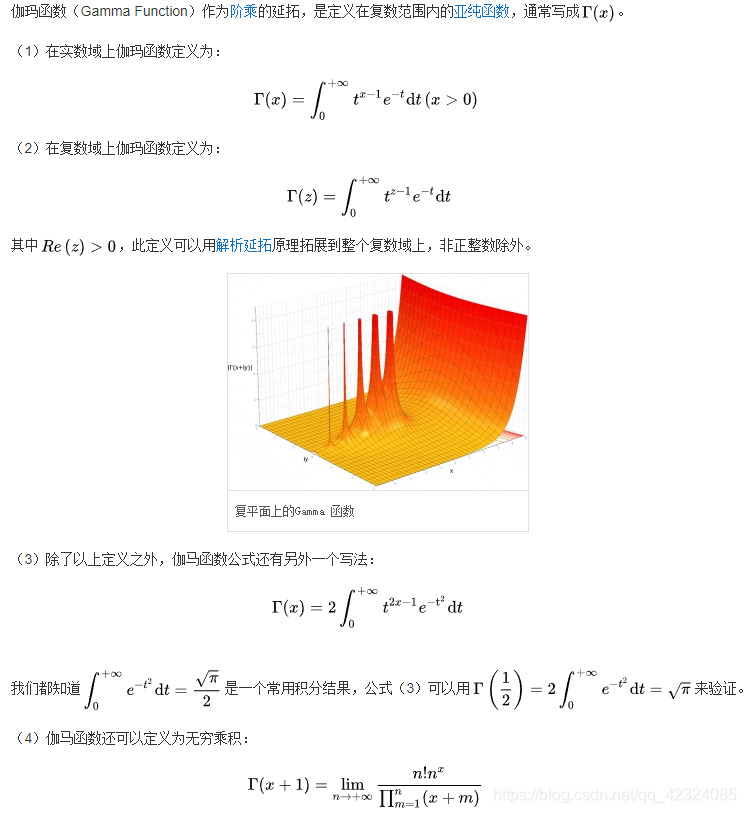
- gamma函数的定义
Gamma函数是复数域内的一个重要函数,其定义主要依赖于阶乘函数的扩展。在实数域中,Gamma函数可以看作是阶乘函数的延伸,它可以对非整数乃至复数进行类似阶乘的运算。
- Gamma函数的基本性质
(1)对称性:Gamma函数是偶函数,即f(x)=f(-x)。
(2)无穷积分收敛性:在一定的条件下,Gamma函数满足无穷积分的收敛性,使得我们可以对无穷级数进行求和计算。
(3)与其他函数的联系:Gamma函数与贝塞尔函数、伽马分布等有着密切的联系,在概率论和数理统计中有着广泛的应用。
- Gamma函数的应用领域
(1)物理领域:在量子力学、核物理等学科中,Gamma函数被广泛用于描述粒子的分布和运动规律。
(2)概率论与数理统计:在概率论和数理统计中,Gamma分布是一种重要的分布形式,其概率密度函数涉及到Gamma函数。
(3)其他领域:在金融、通信等领域,Gamma函数也有着广泛的应用。例如,在金融领域中,Gamma可以用来描述资产价格的波动性。
- Gamma函数的计算方法
计算Gamma函数通常采用积分的方式,例如使用伽马积分公式来求解。同时,也可以通过查找数学软件库或在线工具来获取准确的计算结果。对于特殊情况下的Gamma函数值,也可以通过泰勒级数展开等方法进行计算。
四、总结
本文介绍了gamma函数的定义、基本性质、应用领域以及计算方法。通过本文的介绍,我们可以更好地理解gamma函数在数学和其他学科中的重要性,以及如何在实际应用中使用它。同时,我们也应该注意gamma函数的计算方法和精度问题,以确保在实际应用中能够得到准确的结果。
標籤:
- **关键词**: gamma函数
- 定义
- 基本性质
- 应用领域
- 计算方法
- 阶乘函数
- 复数域
- 偶函数
- 无穷积分
- 收敛性
- 贝塞尔函数
- 伽马分布
- 量子力学
- 核物理
- 概率论
- 数理统计

