一、文章标题


闵可夫斯基距离（Minkowski Distance）


二、文章内容

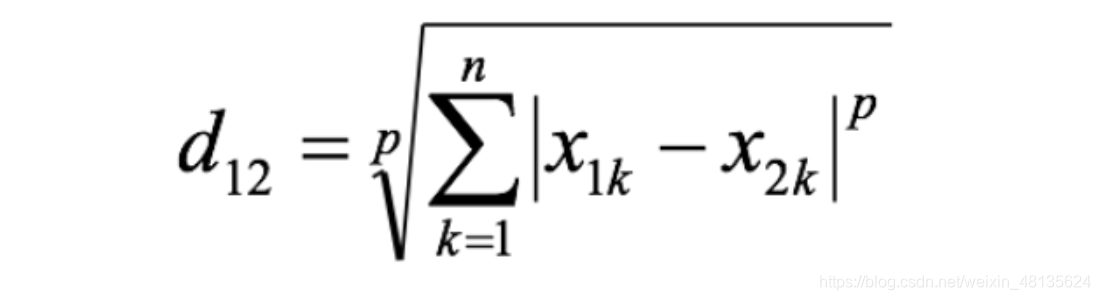
闵可夫斯基距离是一种在多维空间中测量两点之间距离的方法，常用于数据分析和机器学习领域。本文将介绍闵可夫斯基距离的定义、性质和计算方法，并探讨其在实际应用中的重要性。

一、闵可夫斯基距离的定义

闵可夫斯基距离是基于Lp范数定义的距离，它的一般形式为：

D(x,y) = (∑|xi - yi|^p)^(1/p)，其中x和y是两个n维向量，p是一个实数。当p=1时，闵可夫斯基距离就是曼哈顿距离；当p=2时，它就变成了欧氏距离。闵可夫斯基距离通过在不同的空间上（不同范数），能反映出各种空间的差异和联系。

二、闵可夫斯基距离的性质



正确性：对于任何两个点x和y，闵可夫斯基距离都能正确地计算它们之间的距离。



非负性：闵可夫斯基距离总是非负的，即D(x,y)≥0，当且仅当x=y时，D(x,y)=0。



齐次性：对于任意的实数λ，有D(λx, λy) = |λ|D(x, y)。这表示闵可夫斯基距离与空间尺度的变换是成比例的。



三、闵可夫斯基距离的计算方法

闵可夫斯基距离的计算基于向量空间中每个维度上的绝对差值求和后求p次方根。对于两个n维向量x和y，其闵可夫斯基距离可以按照以下步骤计算：



计算每个维度上两个向量的差的绝对值。



将所有维度上的差值绝对值进行求和。



将求和结果进行p次方根运算，得到的就是闵可夫斯基距离。



四、闵可夫斯基距离的应用

闵可夫斯基距离在数据分析和机器学习领域有着广泛的应用。例如，在聚类分析中，可以使用闵可夫斯基距离来衡量不同样本之间的相似度；在图像处理中，可以利用闵可夫斯基距离来比较不同图像之间的差异；在推荐系统中，可以基于用户的行为数据和物品的属性数据，利用闵可夫斯基距离来计算用户与物品之间的相似度等等。

总之，闵可夫斯基距离是一种重要的多维空间距离度量方法，具有广泛的适用性和灵活性。在各种实际应用中，我们可以通过调整参数p来选择适合的度量方式，从而更好地处理和分析数据。