文章标题：OLS（最小二乘法）


在统计学和计量经济学中，OLS（最小二乘法）是一种常用的线性回归分析方法。它通过最小化误差的平方和来寻找最佳函数匹配，以建立因变量和自变量之间的关系。


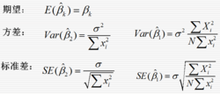
一、OLS的基本概念

OLS回归分析的核心思想是最小化残差平方和。其中，残差指的是观测值与模型预测值之间的差距。OLS的目的是通过优化模型参数来尽可能地减少残差，以使得模型的预测结果更接近真实情况。

二、OLS的应用场景

OLS广泛应用于各种领域，如经济学、金融学、医学等。在经济学中，OLS常用于估计回归模型，以研究经济变量之间的关系。在金融学中，OLS可用于股票价格预测、风险评估等方面。在医学领域，OLS可用于研究生物标志物与疾病之间的关系等。

三、OLS的优点和局限性

优点：


简单易行：OLS的算法相对简单，易于实现。
无偏估计：在一定的假设条件下，OLS能够提供无偏的参数估计。
高效性：OLS能够有效地利用样本信息，提供较为准确的参数估计。

局限性：


假设条件严格：OLS的假设条件较为严格，如线性关系、无异方差性等。如果这些假设不成立，OLS的估计结果可能会产生偏差。
无法处理非线性关系：OLS主要适用于线性关系的研究，对于非线性关系则无法有效处理。
无法考虑其他因素：OLS只能考虑自变量和因变量之间的关系，而无法考虑其他潜在的影响因素。

四、OLS的使用注意事项


数据检查：在使用OLS之前，需要对数据进行检查，以确保数据满足OLS的假设条件。
模型选择：选择合适的模型是使用OLS的关键。需要根据研究目的和数据特点选择合适的模型。
参数估计：在估计参数时，需要注意参数的统计意义和解释。同时，需要关注参数的显著性和置信区间等统计指标。
结果解释：在解释OLS的结果时，需要注意结果的局限性和解释的准确性。不能仅仅根据参数的显著性来判断自变量和因变量之间的关系，还需要考虑其他潜在的影响因素。

总之，OLS是一种常用的线性回归分析方法，具有广泛的应用场景和重要的统计意义。在使用OLS时，需要注意数据检查、模型选择、参数估计和结果解释等方面的问题，以确保得到准确可靠的分析结果。