标题：拓扑结构


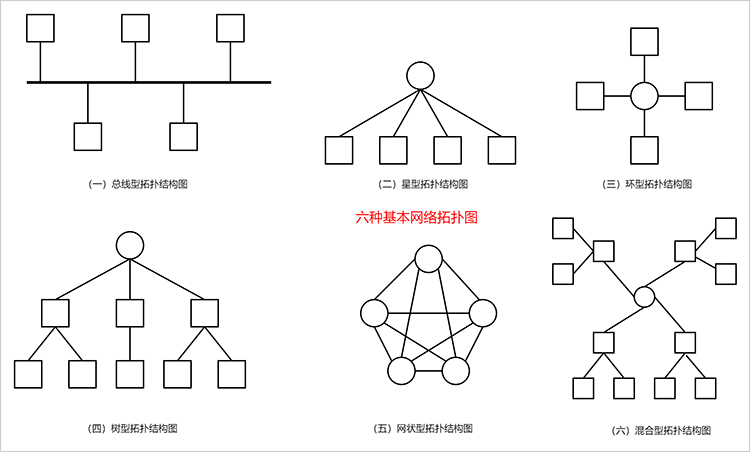
拓扑结构是数学中的一个重要概念，广泛用于图论、计算机科学、物理学和许多其他领域。它是用来描述各种不同事物（如网络、电子电路、几何形状等）的构成方式和空间关系的理论工具。

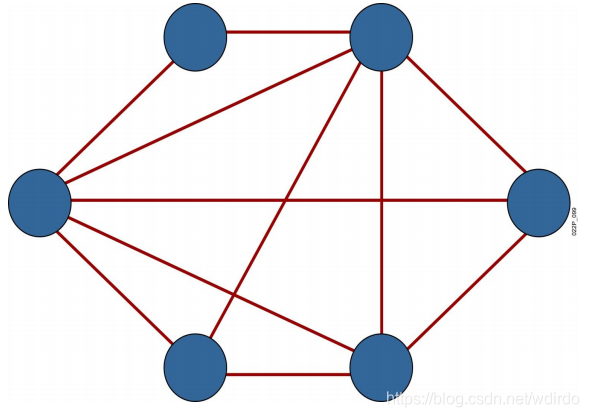
一、拓扑结构的基本概念

拓扑结构主要研究的是空间中点、线、面等元素之间的相互关系和排列方式。在数学中，拓扑结构通常被用来描述一个空间中各个部分之间的连接关系，以及这些连接关系如何影响整个空间的结构。

二、拓扑结构在计算机科学中的应用

在计算机科学中，拓扑结构被广泛应用于网络和图论等领域。在网络中，拓扑结构描述了网络中各个节点之间的连接关系，这种关系决定了网络中信息传输的路径和效率。在图论中，拓扑结构则被用来描述图（即由节点和边组成的图形）的结构和性质。

三、拓扑结构的实际例子



网络拓扑：网络的拓扑结构主要包括星型拓扑、环型拓扑、总线型拓扑等。在实际的网络应用中，网络的拓扑结构通常由其连接的设备和节点的物理布局以及数据传输的路径所决定。



交通网络：城市中的交通网络也是拓扑结构的一个例子。在交通网络中，各个交通节点（如交通枢纽）通过不同的路径相连，形成一个复杂的交通系统。通过对这个交通系统的拓扑结构进行研究，我们可以优化交通布局和提高交通效率。



四、结论

综上所述，拓扑结构是一个非常实用的概念，在许多领域都有着广泛的应用。通过了解和分析一个系统的拓扑结构，我们可以更好地理解这个系统的性质和特点，进而进行更有效的设计和优化。

以上是有关拓扑结构的简单介绍，希望能够对您有所启发和帮助。如需了解更多关于拓扑结构的知识和应用，建议查阅相关书籍或文献资料。