残差的定义
主机域名文章
2024-12-11 17:40
973
标题: 残差的定义
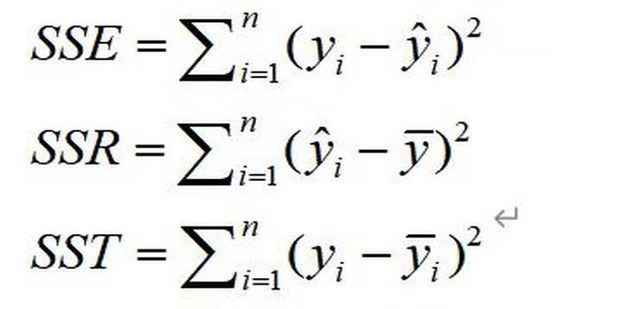
在统计学和数据分析中,残差是一个非常重要的概念。它通常用于描述模型预测值与实际观测值之间的差距。这种差距可以帮助我们理解模型的准确性和可靠性,以及在模型改进和优化中发挥作用。

一、什么是残差?

残差(Residual)是指观测值与模型预测值之间的差距,一般用观测值减去预测值得到。在回归分析中,这个差距常被用来衡量模型对数据的拟合程度。
二、残差的计算方法
残差的计算通常在回归分析中应用。当我们使用线性回归模型来描述两个或多个变量之间的关系时,我们通常会用模型的预测值与实际观测值进行对比,并计算它们的差异,即残差。在简单线性回归模型中,每个观测值的残差可以这样计算:
残差 = 实际观测值 - 预测值
在多元回归模型中,计算方法类似,只是涉及到更多的变量和更复杂的计算过程。
三、残差的作用
-
模型评估:残差可以帮助我们评估模型的准确性和可靠性。如果大部分残差的绝对值都较小,且呈现正态分布的形态,那么这表明模型可能比较准确;相反,如果存在大量大残差或者有明显的残差分布不规律的现象,则可能表示模型存在问题,需要进一步改进或优化。
-
异常值检测:残差还可以帮助我们检测数据中的异常值或误差。例如,在时间序列分析中,如果一个观测值的残差特别大,那么可能表明该数据点存在测量误差或其他问题。
-
模型优化:在模型的训练和调整过程中,我们可以使用残差来帮助优化模型的参数和结构,从而得到更准确的预测结果。
总结起来,残差是一个非常有用的概念,它不仅可以帮助我们评估模型的准确性和可靠性,还可以用于异常值检测和模型优化。在数据分析中,我们经常使用残差来改进和优化我们的模型,从而得到更准确的预测结果。
Label:
- 关键词:残差
- 模型预测值
- 实际观测值
- 回归分析
- 正态分布
- 异常值检测
- 模型优化

