一、文章标题


残差的计算公式

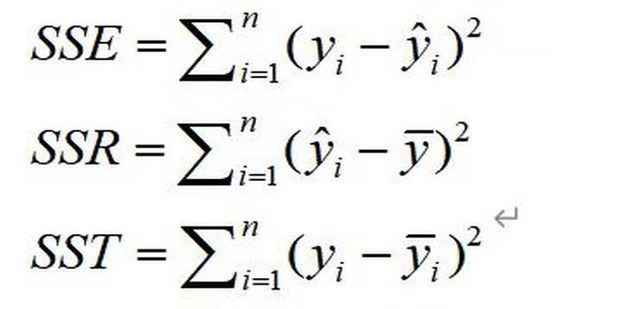
二、文章内容

在统计学和数据分析中，残差是一个非常重要的概念。它表示的是观测值与预测值之间的差异。本文将详细介绍残差的计算公式及其应用。

1. 什么是残差？

残差，也称为剩余值，是实际观测值与通过模型预测的值之间的差异。在回归分析中，残差是因变量与根据自变量和回归方程预测的值之间的差距。

2. 残差的计算公式

残差的计算公式相对简单，一般用于线性回归分析。对于一组数据，我们首先通过回归方程得到预测值，然后用实际观测值减去预测值，即可得到残差。

对于一元线性回归，假设我们有一个自变量x和一个因变量y，通过回归分析得到的回归方程为：y^ = ax + b（其中y^为预测值）。那么残差的计算公式为：残差 = 实际观测值 - 预测值 = y - (ax + b)。

对于多元线性回归，残差的计算方法类似，只是需要考虑多个自变量。每个自变量都会对预测值产生影响，因此需要将这些影响综合考虑进来。

3. 残差的应用

残差在统计学和数据分析中有着广泛的应用。首先，残差可以帮助我们了解模型的拟合程度。如果残差较大，说明实际观测值与预测值之间的差异较大，可能需要进一步优化模型。其次，残差还可以用于检测异常值和误差。当残差的绝对值过大时，可能说明存在异常观测值或模型误差，需要进行进一步分析。

此外，残差还可以用于预测和推断。通过对残差的分析，我们可以了解因变量的变化规律和趋势，从而对未来的观测值进行预测。同时，残差还可以帮助我们推断自变量与因变量之间的关系，为进一步的研究提供依据。

总之，残差是数据分析中一个非常重要的概念。通过了解残差的计算公式及其应用，我们可以更好地理解数据之间的关系和规律，为进一步的研究和决策提供依据。