一阶差分


一、什么是差分


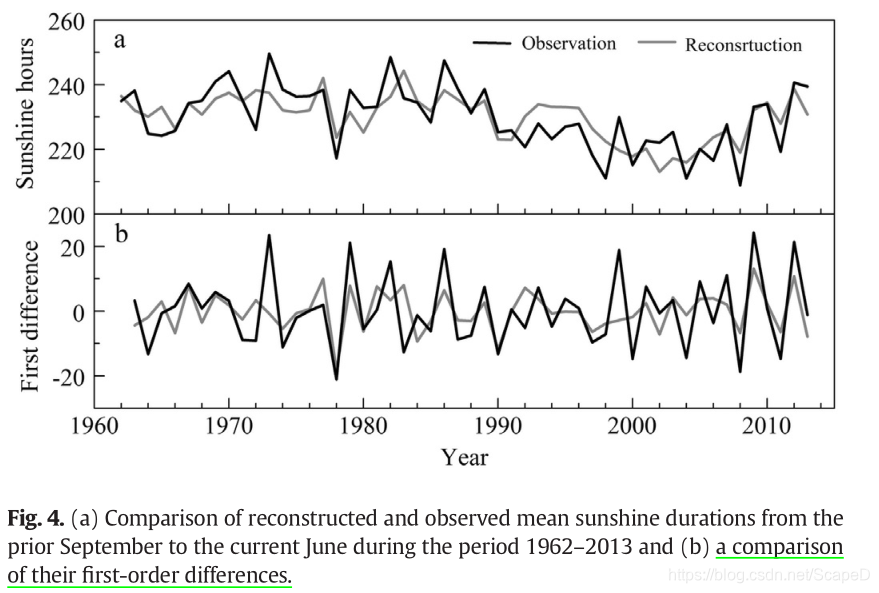
差分，在数学和统计学中，通常指的是两个数据点之间的差异。在时间序列分析中，一阶差分指的是将当前时间点的数据与前一个时间点的数据进行相减，从而得到差值。这种差分操作可以帮助我们更好地理解数据的动态变化情况。

二、一阶差分的应用

一阶差分在经济学、金融学、统计学等领域有着广泛的应用。在时间序列分析中，一阶差分常用于处理非平稳数据，通过差分操作将非平稳数据转化为平稳数据，从而更好地进行预测和建模。

三、一阶差分的计算方法

一阶差分的计算方法非常简单，只需要将当前时间点的数据减去前一个时间点的数据即可。在具体计算中，我们需要根据实际情况选择合适的时间间隔和起始点。对于时间序列数据，通常选择相邻的时间点进行差分计算。对于其他类型的数据，则需要根据具体情况进行选择。

四、一阶差分的意义

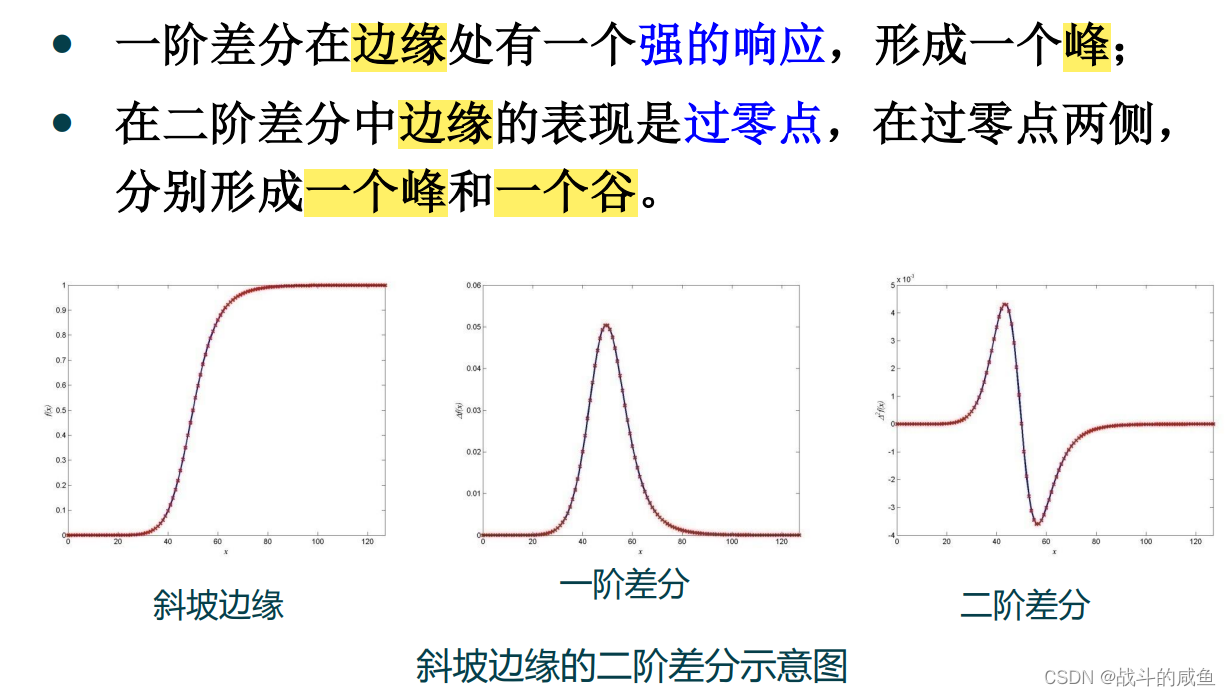
一阶差分可以帮助我们更好地理解数据的动态变化情况。通过对时间序列数据进行一阶差分，我们可以得到数据的增长速度和趋势变化情况，从而更好地预测未来的变化趋势。此外，一阶差分还可以帮助我们消除数据中的季节性波动和周期性变化，使得数据更加平稳，有利于进行预测和建模。

五、一阶差分的实际应用

一阶差分在实际应用中有着广泛的应用场景。例如，在股票价格预测中，我们可以通过对股票价格进行一阶差分来分析股票价格的波动情况和趋势变化情况，从而更好地进行投资决策。在气象学中，一阶差分可以用于分析气温、降雨量等气象数据的动态变化情况，帮助我们更好地预测天气变化趋势。此外，一阶差分还可以应用于人口统计、经济增长率等领域的分析和预测。

总之，一阶差分是一种重要的数据处理和分析方法，它可以帮助我们更好地理解数据的动态变化情况，消除数据中的季节性波动和周期性变化，从而更好地进行预测和建模。在实际应用中，我们需要根据具体情况选择合适的时间间隔和起始点进行一阶差分计算。