SVD分解


SVD（奇异值分解）是一种在机器学习、信号处理和数据分析等领域中广泛使用的数学工具。它可以将一个复杂的矩阵分解为三个更简单的矩阵，即左奇异向量、奇异值和右奇异向量。


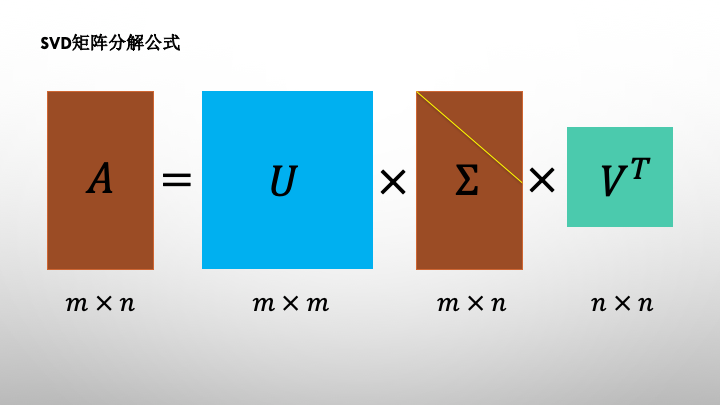
一、SVD分解的基本概念

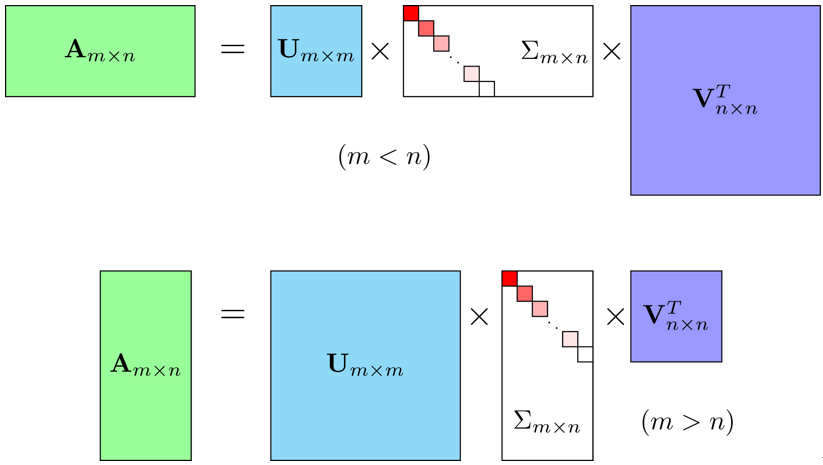
对于任意一个m×n的矩阵A，SVD分解可以表示为A=UΣV'，其中U是m×m的左奇异矩阵，Σ是m×n的矩阵（其对角线上的元素为奇异值，其他元素为0），V是n×n的右奇异矩阵。'表示转置操作。

二、SVD分解的物理意义

SVD分解的物理意义在于揭示了矩阵A的内在结构。左奇异向量U和右奇异向量V分别描述了矩阵A在行空间和列空间上的主要变化方向，而奇异值则是这些变化的重要程度度量。

三、SVD分解的应用


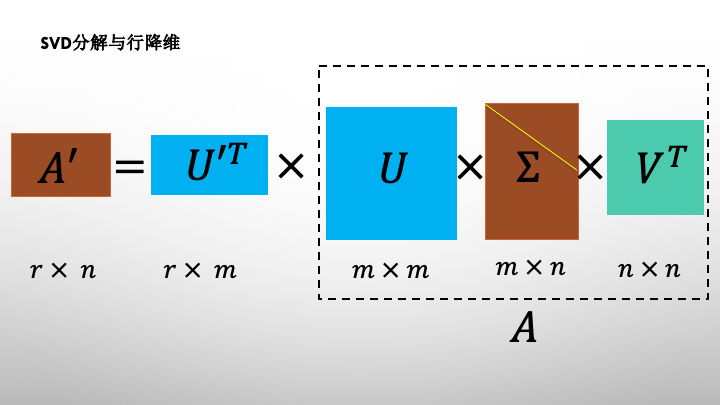
数据降维：通过SVD分解，可以将原始的高维数据降维到低维空间，同时保留大部分信息。这在处理高维数据时非常有用。
推荐系统：SVD可以用于构建推荐系统，通过用户-物品矩阵的SVD分解，可以预测用户对未见过物品的喜好程度。
图像处理：SVD可以用于图像压缩和去噪等任务。通过SVD分解，可以将图像的冗余信息去除，只保留主要的信息，从而达到压缩的目的。

四、SVD分解的算法实现

SVD分解的算法实现较为复杂，需要一定的数学基础。在实际应用中，通常会使用一些优化过的库或工具来实现SVD分解，如Python中的NumPy和SciPy库。

五、总结

SVD分解是一种强大的数学工具，可以用于处理各种复杂的问题。它通过将一个复杂的矩阵分解为三个简单的矩阵，揭示了矩阵的内在结构，并提供了许多有用的信息。在机器学习、信号处理和数据分析等领域中，SVD分解都有着广泛的应用。

以上就是关于SVD分解的简要介绍和解释，希望对你有所帮助。如需深入了解SVD分解的相关知识和应用，建议查阅相关的教材、论文或参考书籍。