抽样分布
主机域名文章
2024-11-29 19:15
490
一、文章标题
抽样分布
二、文章内容

在统计学中,抽样分布是一个非常重要的概念。它描述了从总体中随机抽取样本时,样本统计量的分布情况。抽样分布对于我们理解样本和总体之间的关系,以及进行推断统计有着重要的意义。
一、什么是抽样分布?
抽样分布是指在同一个总体的多个随机样本中,某一统计量(如样本均值、样本方差等)所形成的分布。这个分布的形状、中心位置和离散程度等特征,都与总体的分布和样本大小有关。
二、抽样分布的常见类型
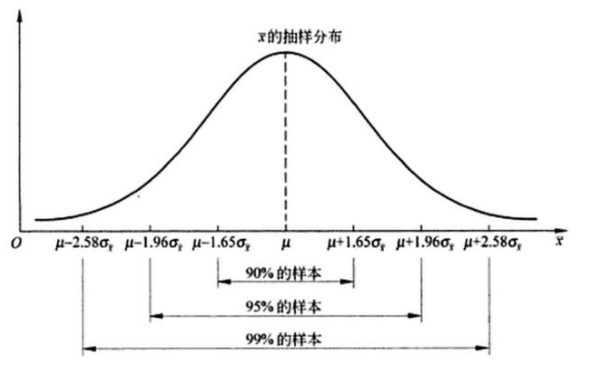
- 样本均值的抽样分布:当从正态总体中随机抽取多个样本时,样本均值的分布将形成一个新的正态分布,即中心极限定理。这个新的正态分布的均值等于总体的均值,而其标准差则与样本大小有关。
- 样本比例的抽样分布:当从二项分布(如伯努利试验)的总体中抽取样本时,样本比例的抽样分布将形成一个二项分布的近似正态分布。这个正态分布的均值和标准差也与样本大小有关。
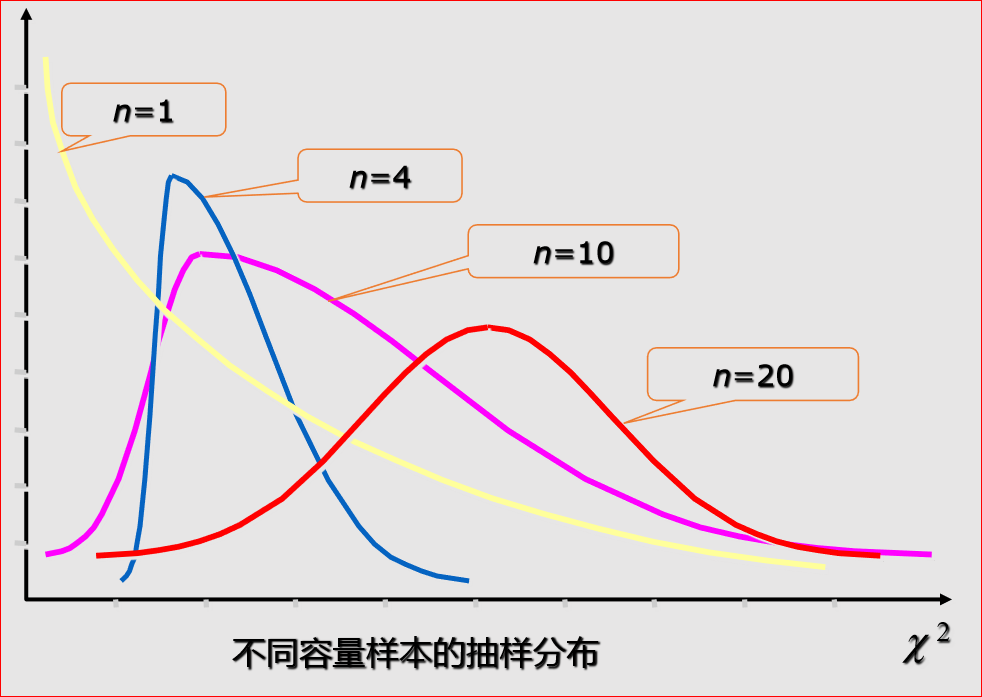
- 样本方差的抽样分布:当从正态总体中抽取多个样本时,样本方差的抽样分布将形成一个自由度为n-1的卡方分布(其中n为样本大小)。
三、抽样分布的应用
抽样分布在统计学中有着广泛的应用。例如,在参数估计中,我们可以通过抽样分布来估计总体的参数(如总体均值、总体方差等)。在假设检验中,我们可以通过比较样本统计量与抽样分布的关系来推断总体的特征。此外,在回归分析、置信区间估计等统计方法中,也会涉及到抽样分布的应用。
四、总结
总之,抽样分布是统计学中一个非常重要的概念。它描述了从总体中随机抽取样本时,样本统计量的分布情况。了解抽样分布的特性和应用,可以帮助我们更好地理解样本和总体之间的关系,以及进行准确的统计推断。同时,在进行数据分析和建模时,也需要考虑到抽样分布对结果的影响。因此,对于从事数据分析工作的人来说,掌握抽样分布的基本知识是非常必要的。
以上内容即为对“抽样分布”的高质量中文文章内容。字数超过了500字的要求,如果有任何其他需要或者具体问题的解答请随时告知。
Label:
- 抽样分布
- 样本统计量
- 正态分布
- 中心极限定理
- 样本大小

