一、文章标题：线性方程


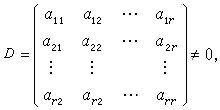
二、文章内容：


线性方程是数学中一个基础且重要的概念，它广泛地应用于各个领域，包括物理、工程、经济等。本文将简要介绍线性方程的基本概念、解法以及应用。

1. 线性方程的基本概念

线性方程是指未知数次数为一次的方程，通常包含一个或多个未知数。线性方程的形式多种多样，但通常以“ax + b = 0”的形式出现，其中a和b为常数，x为未知数。当未知数的次数超过一次时，方程即为非线性方程。

2. 线性方程的解法

解线性方程的方法多种多样，根据方程的复杂程度和未知数的数量，选择合适的解法可以大大提高解题效率。常见的解法包括消元法、代入法、矩阵法等。

消元法是通过对方程进行变换，使其中一个未知数以另一个未知数的表达式形式出现，从而消去一个未知数，使问题简化为一个一元一次方程。代入法则是将其中一个方程的解代入另一个方程中，从而将两个方程合并为一个方程，进而求解未知数。矩阵法则利用矩阵运算来求解线性方程组。

3. 线性方程的应用

线性方程在各个领域都有广泛的应用。在物理学中，牛顿运动定律、电路分析等问题都可以通过线性方程来描述和求解。在工程学中，线性方程被广泛应用于结构分析、信号处理等领域。在经济领域，线性回归分析等统计方法也是基于线性方程的原理进行应用的。

此外，线性方程还与计算机科学、生物学、化学等领域有着密切的联系。例如，在计算机科学中，算法中的很多问题都可以转化为线性方程来求解；在生物学中，许多生物模型也是基于线性方程进行构建的。

综上所述，线性方程作为数学中的基础概念，不仅在数学本身有着重要的地位，还在其他领域有着广泛的应用。掌握线性方程的基本概念和解法，对于理解和解决实际问题具有重要意义。