一、方向向量的概念


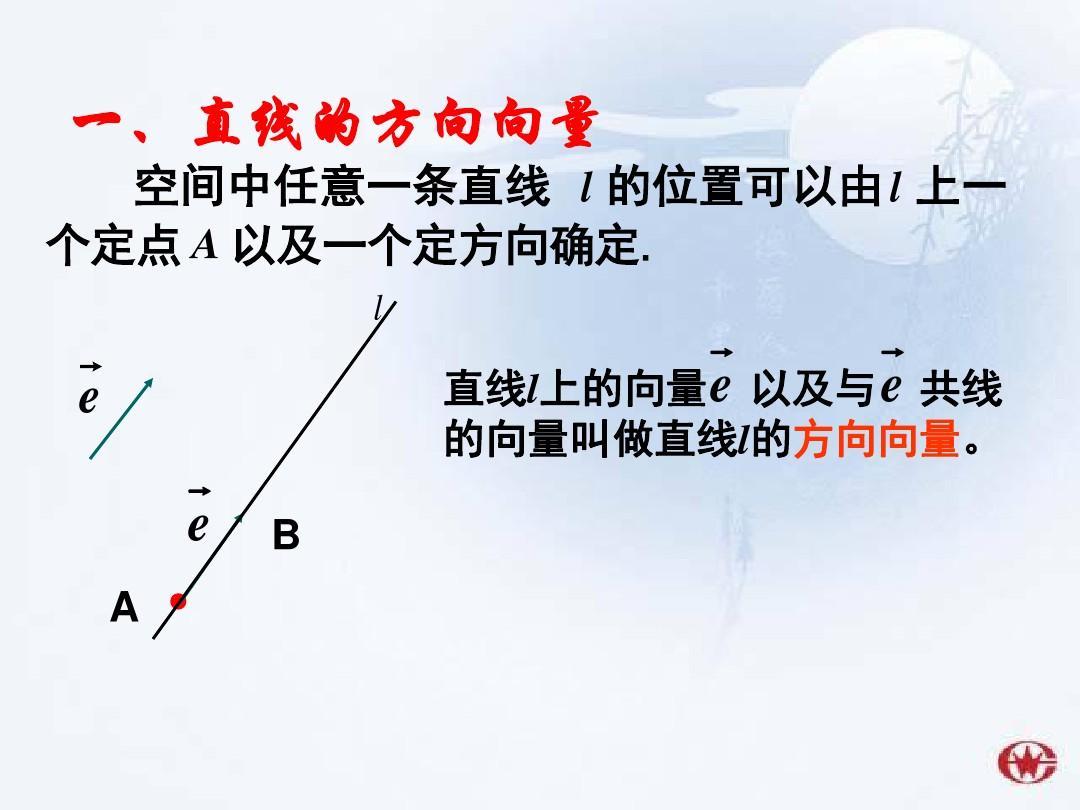
在数学和物理中，方向向量是一个重要的概念。它通常用于描述空间中某一点的方向或变化趋势。在二维空间中，方向向量可以表示为一个点相对于原点的位置变化；在三维空间中，方向向量则更加复杂，但同样可以表示空间中某一点或某条线的方向。

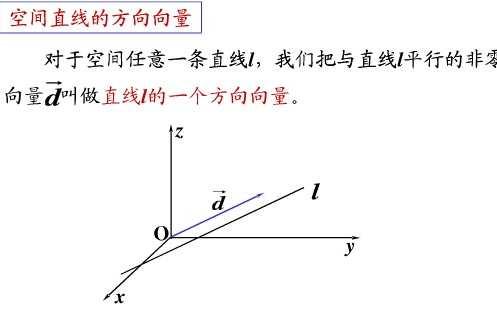
二、方向向量的表示

方向向量通常用箭头表示，箭头的起点表示原点，箭头的方向和长度则表示了方向向量的方向和大小。在数学中，方向向量通常用有序数对或有序数组来表示，例如在二维空间中，我们可以使用两个实数来表示一个方向向量；在三维空间中，我们需要使用三个实数来表示一个方向向量。

三、方向向量的应用

方向向量在数学、物理和工程领域都有着广泛的应用。例如，在几何学中，我们可以使用方向向量来描述线段或曲线的切线方向；在物理学中，我们可以使用方向向量来描述物体的运动方向和速度；在工程学中，我们可以使用方向向量来描述力的作用方向和大小等。

四、如何计算方向向量

计算方向向量的方法因具体问题而异，但通常涉及到向量的加减法、数乘等基本运算。例如，如果我们有两个点A和B，那么从A到B的向量就是B的坐标减去A的坐标得到的结果，这就是一个简单的方向向量计算。在更复杂的情况下，可能需要用到更复杂的数学运算来得到一个精确的方向向量。

五、总结

总的来说，方向向量是一个非常有用的概念，它不仅在数学和物理中有着广泛的应用，而且在日常生活和工作中也有着重要的应用价值。通过学习方向向量的概念和计算方法，我们可以更好地理解和描述空间中的变化趋势和方向关系。同时，我们也可以利用方向向量来解决一些实际问题，如力的合成与分解、运动轨迹的描述等。因此，掌握方向向量的知识和技能对于提高我们的数学素养和解决实际问题具有重要意义。

以上内容仅是简略的介绍和阐述，如果需要更深入的学习和研究，建议查阅相关教材和资料。同时，也欢迎大家在实践和学习过程中不断探索和创新，将这个重要的概念应用于更多的领域和场景中。