一、离散度（Dispersity）


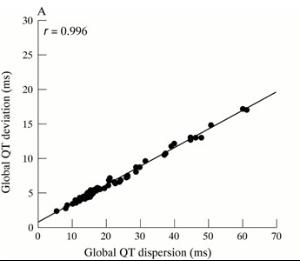
离散度，是统计学中一个重要的概念，用于描述一组数据的分散程度。在许多领域，如数据分析、机器学习等，离散度都扮演着重要的角色。


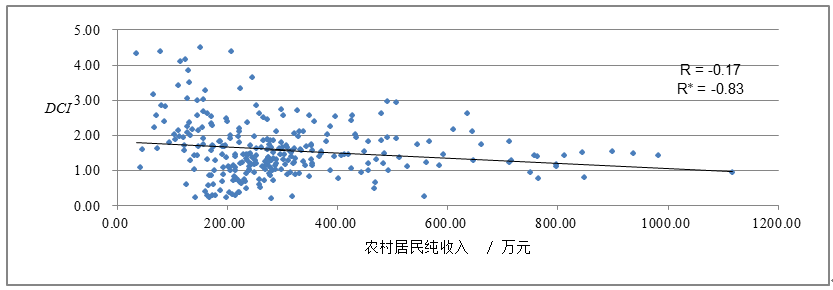
1. 离散度的定义

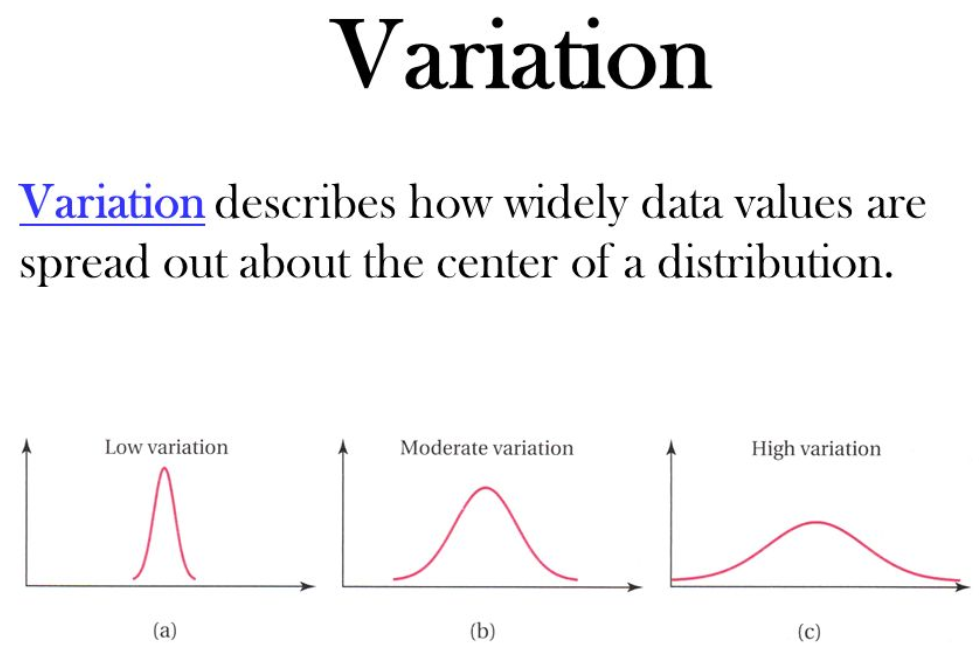
离散度通常用来量化数据的分布情况。在统计学中，离散度常常通过标准差、方差等指标来衡量。这些指标可以帮助我们了解数据的分布是否集中或分散。

2. 离散度的类型

离散度可以分为多种类型，包括但不限于：


样本的离散度：描述样本数据间的差异程度。
总体离散度：描述整个数据集的分散程度。
概率分布的离散度：在概率论中，用来描述随机变量可能取值的分布情况。

3. 离散度的应用

在现实生活中，离散度的应用十分广泛。

在数据分析中，我们可以通过分析数据的离散度来了解数据的稳定性、波动性等特性。例如，在股票市场中，我们可以通过分析股票价格的离散度来预测市场的走势。

在机器学习中，离散度也是一个重要的概念。例如，在聚类算法中，我们常常需要计算不同簇之间的离散度来评估聚类的效果。

4. 如何计算离散度

计算离散度通常需要使用统计学的方法。例如，计算一组数据的标准差就是离散度的一种常见方法。标准差越大，说明数据越分散；标准差越小，说明数据越集中。

除了标准差之外，还有方差、四分位距等其他指标可以用来衡量离散度。这些指标各有特点，可以根据具体的应用场景选择合适的指标。

5. 总结

总的来说，离散度是一个非常重要的概念，它可以帮助我们了解数据的分布情况、稳定性以及波动性等特性。在数据分析、机器学习等领域中，离散度都有着广泛的应用。通过计算和分析离散度，我们可以更好地理解数据、优化模型并做出更准确的预测。