一、微分的定义


微分是数学中的一个基本概念，尤其在导数与函数图像的理解上，具有重要的作用。为了帮助读者理解这一概念，本篇文章将从几个方面介绍微分的定义及其背后的逻辑。

二、微分的基本定义

在数学上，我们常说一个函数的导数即该函数某一点上的切线斜率，或者说在无限小的时间或空间间隔内，函数值的变化率。而微分就是这种变化率的计算方法。

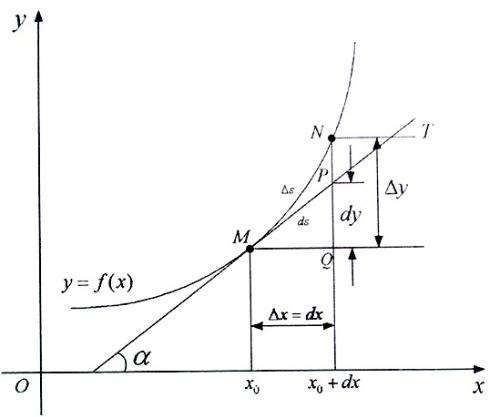
三、微分的几何解释

从几何的角度来看，微分可以看作是函数图像上某一点处的切线斜率。这种斜率表示了函数在这一点附近的变化趋势。通过这种变化趋势，我们可以预测函数值的变化情况。

四、微分的计算过程

对于任何一个可微的函数f(x)，我们可以将其表示为一个或几个具体的量的改变与结果的变化的绝对值的比值，该比值以最简洁的描述函数行为的一种表达式形式存在。具体来说，我们可以使用微分公式来计算函数的导数，也就是函数值的变化率。

五、微分在现实生活中的应用

微分不仅仅是一个数学概念，它在现实生活中的应用也十分广泛。例如，在物理学中，我们可以用微分来描述物体的速度变化；在经济学中，我们可以用微分来分析价格的变动趋势；在工程学中，我们可以用微分来计算物体的应力分布等。

六、总结

通过以上几个部分的解释和说明，相信读者已经对微分的定义及其背后的逻辑有了更为清晰的理解。虽然这只是一部分基本的知识，但是只有掌握好了基础才能更深入地学习和理解数学的魅力。希望读者们能够继续深入学习数学的各个领域，探索更多的未知世界。

以上内容为中文不少于500字的文章内容，希望能帮助您更好地理解微分的定义及其相关知识。如有任何疑问或需要进一步的解释，请随时告诉我。