一、文章标题


btree 简介与实现

二、文章内容

在计算机科学中，B树是一种特殊的树状数据结构，被广泛用于存储大量有序的数据并快速查询它们。它的特点是树内数据不仅可向上递增，也支持根据关键码和特定范围的数据检索节点中的信息。以下将对B树的定义、应用及实现方法进行简要阐述。

一、B树定义

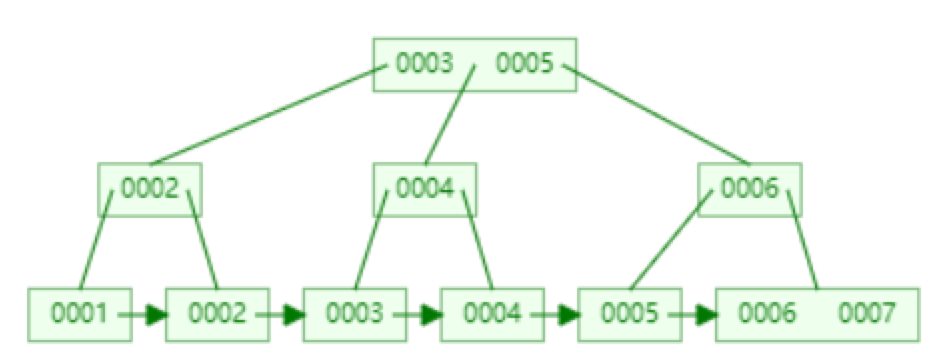
B树是一种多叉平衡树，其每个节点可以拥有多个子节点。在B树中，每个节点包含多个关键字和指向子节点的指针。每个关键字对应一个子节点的范围，因此B树能够快速地根据关键字进行搜索。B树的特性使得其在进行磁盘I/O操作时具有很高的效率，因此常用于数据库索引等场景。

二、B树的应用

B树在数据库领域有着广泛的应用，如MySQL等数据库系统就采用了B树或其变种作为索引结构。此外，B树还常用于文件系统、搜索引擎等场景，以提高大量数据的读写效率。通过将数据的查找路径和访问顺序结合到树的节点结构中，B树能大大减少I/O操作的次数，提高系统性能。

三、B树的实现

B树的实现主要涉及节点的定义、插入、删除和查找等操作。在实现过程中，需要遵循B树的特性，如每个节点的子节点数量有一定范围限制（例如在某个最大值与最小值之间），同时满足节点的关键字数与其度数之间有固定关系等。此外，在实现过程中还需要考虑树的平衡性、磁盘I/O操作的效率等因素。

四、具体实现步骤


定义节点结构：根据B树的特性，定义节点的结构，包括关键字和子节点的指针等。
插入操作：当需要插入新的数据时，从根节点开始查找合适的位置进行插入。如果插入导致节点关键字数量超过一定阈值，需要进行分裂操作以保持树的平衡性。
删除操作：当需要删除数据时，同样从根节点开始查找并删除对应的关键字。如果删除导致节点关键字数量低于一定阈值，需要进行合并或分裂操作以保持树的平衡性。
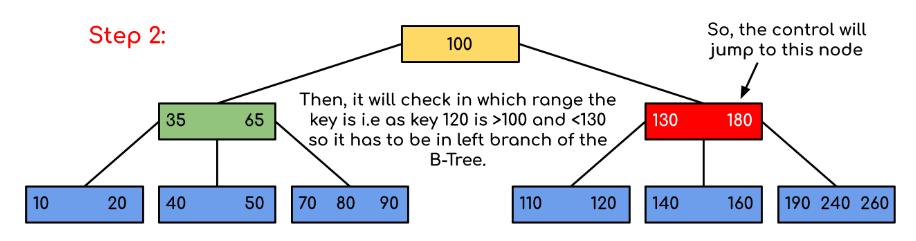
查找操作：通过从根节点开始依次比较关键字和指针来查找目标数据。由于B树是平衡的，所以查找效率较高。
平衡调整：在插入和删除操作后，需要对树进行平衡调整以保持其特性。这包括分裂、合并和重新分配子节点等操作。

总之，B树是一种重要的数据结构，具有广泛的应用场景和高效的性能表现。掌握其定义、应用和实现方法对于计算机科学的学习具有重要意义。以上是对B树的基础介绍与简单实现方法的介绍，如果想要更深入地理解与运用，还需对算法细节与相关变体进行学习与掌握。