狄拉克函数：深度理解其定义与应用


一、狄拉克函数概述

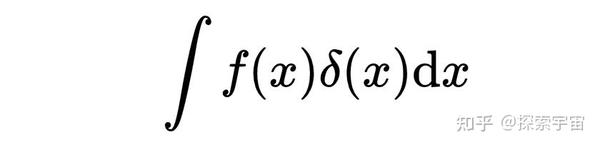
狄拉克函数（Dirac Delta Function），或称冲击函数，在物理学和信号处理等领域中有着广泛的应用。它是一种特殊的数学函数，具有许多独特的性质和特点。本文将深入探讨狄拉克函数的定义、性质、应用等方面，帮助读者更好地理解这一重要的数学工具。

二、狄拉克函数的定义

狄拉克函数通常被定义为一种特殊的函数，其值在所有点上均为零，除了在原点处值为1。其正式定义可以通过各种不同的方法进行表述，其中最为常见的可能是“当自变量与某一确定值相等的时刻取值为无穷大，其他时刻取值为零”。这种特性使得狄拉克函数在数学和物理领域中具有独特的地位。

三、狄拉克函数的性质

狄拉克函数具有许多重要的性质，包括正交性、奇偶性、以及它在傅里叶变换和拉普拉斯变换等中的应用。它是一组正交基的基底，可以用于描述许多复杂的物理现象。此外，狄拉克函数的积分和卷积等运算也具有特殊的性质，这些性质在信号处理、电路分析和微分方程求解等领域有着广泛的应用。

四、狄拉克函数的应用


信号处理：在通信系统和音频处理等领域中，狄拉克函数常被用于表示离散的时间或频率样本。此外，在模拟和数字信号处理中，狄拉克函数也常被用作脉冲响应或滤波器的单位样本。
物理学：在量子力学中，狄拉克函数用于描述波函数的突变点，特别是在波函数发生跳变时起着关键作用。此外，在相对论物理学中，狄拉克函数也扮演着重要的角色。
数学：在微分方程的求解过程中，狄拉克函数常常作为初始条件或边界条件出现。此外，在傅里叶变换和拉普拉斯变换等数学运算中，狄拉克函数也具有重要的应用价值。

五、总结

总之，狄拉克函数作为一种特殊的数学工具，在各个领域中都有着广泛的应用。通过深入理解其定义和性质，我们可以更好地利用这一工具来描述和分析复杂的物理现象和数学问题。同时，对于学习和掌握信号处理、电路分析等知识的学生来说，掌握狄拉克函数也具有重要意义。未来随着科技的不断发展和应用需求的增加，相信狄拉克函数的应用领域将更加广泛和深入。