一、对称矩阵的性质


在数学领域，对称矩阵是一种特殊的矩阵，其特性在于其转置矩阵与自身相等。这种矩阵在许多领域都有广泛的应用，包括线性代数、物理、计算机科学等。以下，我们将深入探讨对称矩阵的一些重要性质。

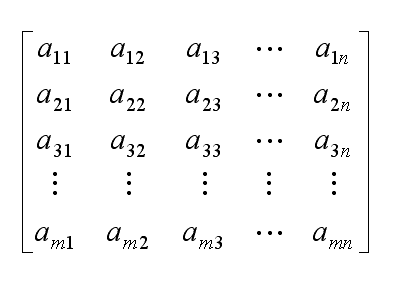
1. 定义与基本性质

对称矩阵是一个方阵，其转置矩阵与原矩阵相等。数学上，我们可以将其表示为 A^T = A，其中 A 是一个 m×n 的矩阵。对于对称矩阵来说，其维度必须是正方形（即行数等于列数）。

2. 特征值与特征向量

对称矩阵的特征值和特征向量具有特殊的性质。其所有的特征值都是实数，且每个特征值都对应一组完整的线性无关的特征向量。这一特性使得对称矩阵在许多物理和工程问题中非常有用。

3. 正定性

如果对称矩阵的所有特征值都是正数，那么这个对称矩阵就是正定的。正定对称矩阵在许多优化问题中都有重要的应用，例如在二次型优化问题中。

4. 逆矩阵与行列式

对于可逆的对称矩阵（即存在逆矩阵的对称矩阵），其逆矩阵也是对称的。此外，对称矩阵的行列式是实数。这些性质使得对称矩阵在许多计算中都非常有用。

5. 空间变换

在空间变换中，对称矩阵可以用来描述线性变换的几何性质。例如，在二维空间中，一个对称矩阵可以描述一个旋转或反射的变换。在三维空间中，这种变换可能更加复杂，但仍然可以通过对称矩阵来描述。

6. 实际应用

由于对称矩阵的特殊性质，它在许多领域都有广泛的应用。例如，在物理学中，它可以用来描述波函数的性质；在计算机科学中，它可以用来描述图像处理和计算机视觉中的某些问题；在经济学和金融学中，它可以用来描述投资组合的优化问题等。

总的来说，对称矩阵是一种非常重要的数学工具，具有许多独特的性质和广泛的应用。了解这些性质和应用可以帮助我们更好地理解和使用这种特殊的矩阵。