标题： 反余切函数


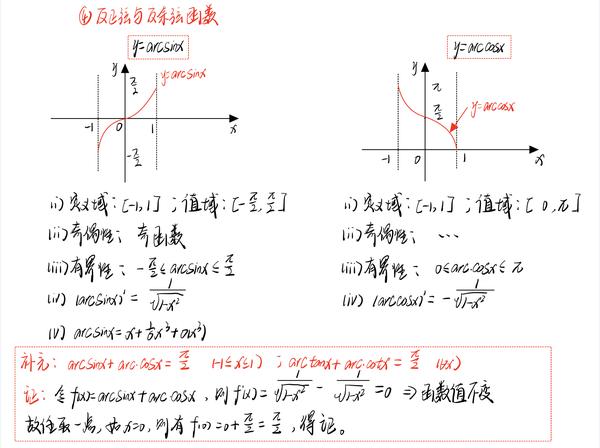
在数学中，反余切函数（Arcsine function）是一个非常重要的函数，它是正弦函数的反函数。通过这个函数，我们可以方便地找出特定角度的余弦值。本文将简要介绍反余切函数的定义、性质以及一些常见应用。


一、反余切函数的定义

反余切函数是正弦函数的反函数，其定义域为[-π/2, π/2]，值域为实数集R。对于任意实数x，反余切函数arcsin(x)表示一个角度θ（单位为弧度），该角度的正弦值为x。因此，我们可以利用反余切函数将余弦值转化为角度值。

二、反余切函数的性质

反余切函数具有一些重要的性质。首先，它是单调递增的，这意味着随着x的增大，函数值也会随之增大。其次，当x为正时，arcsin(x)的取值范围为[0, π/2]；当x为负时，其取值范围为[-π/2, 0]。此外，反余切函数还具有奇偶性、周期性等性质。

三、反余切函数的应用

反余切函数在许多领域都有广泛的应用。例如，在物理中，它被用来描述波的振幅和相位之间的关系；在工程中，它被用来计算信号的相位差等。此外，在统计学和数据分析中，反余切函数也扮演着重要的角色。例如，我们可以利用它来计算概率密度函数的分布情况等。

四、常见问题及解决方法

在使用反余切函数时，可能会遇到一些问题。例如，由于反余切函数的定义域有限制（[-π/2, π/2]），因此在进行计算时需要注意输入值的范围。另外，由于计算机中通常使用弧度制表示角度，因此在进行计算时需要将角度转换为弧度。对于这些问题，我们可以通过仔细阅读相关文档、查阅资料或寻求专业人士的帮助来解决。

总之，反余切函数是一个非常有用的数学工具，它在许多领域都有广泛的应用。通过了解其定义、性质和应用，我们可以更好地运用这个函数来解决实际问题。