一、文章标题


logax的导数详解


二、文章内容

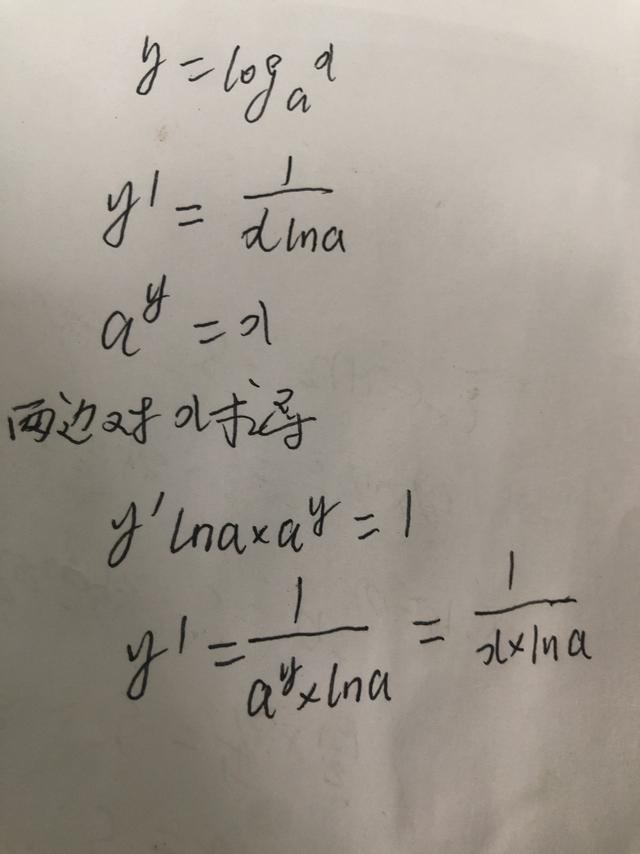
在数学中，导数是一个非常重要的概念，它描述了函数在某一点的变化率。而在实际应用中，经常需要对logarithmic（对数）函数的导数进行求解，其中包括了以任意底数为底的对数函数logax。本文将详细介绍logax的导数计算方法。

首先，我们需要了解对数函数的基本形式和性质。对数函数logax可以表示为以a为底x的对数，其中a是一个正常数且a>0，x是自变量。对数函数在数学和实际生活中有着广泛的应用，如复利计算、统计等。

接下来，我们要求解logax的导数。在微积分中，对数函数的导数通常用链式法则来求解。对于logax的导数，我们可以使用自然对数的底数e来作为桥梁进行推导。具体步骤如下：

步骤一：令t=x^n（n为常数），然后取自然对数ln(t)。此时的导数为dt/dt。将ln(t)再次展开得到对数形式的x，接着分别计算各项的导数，并用链式法则进行组合。

步骤二：根据链式法则，对于复合函数f(g(x))的导数，等于f'(g(x))乘以g'(x)。在logax的导数计算中，我们首先计算ln(t)的导数（即1/t），然后乘以t关于x的导数（即n*x^(n-1)）。

步骤三：将上述两步的结果相乘，即可得到logax的导数。具体来说，对于以e为底的对数函数lnx（即logex），其导数为1/x；而对于以任意正实数a为底的对数函数logax（其中a≠e），其导数为1/(x*ln(a))。

通过以上步骤，我们得到了logax的导数的详细推导过程。在实际应用中，当需要求解以其他底数为底的对数函数的导数时，也可以按照类似的步骤进行推导。

掌握logax的导数的计算方法对于理解和应用微积分理论具有重要意义。此外，对数函数在各种实际场景中也有着广泛的应用价值。因此，熟练掌握并灵活运用本篇文章介绍的求导方法将有助于更好地解决实际问题。

以上就是关于logax的导数的详细介绍和推导过程。希望能够帮助您更好地理解和掌握这一重要概念。