文章标题：反余弦函数图像


Markdown格式排版下的高质量文章


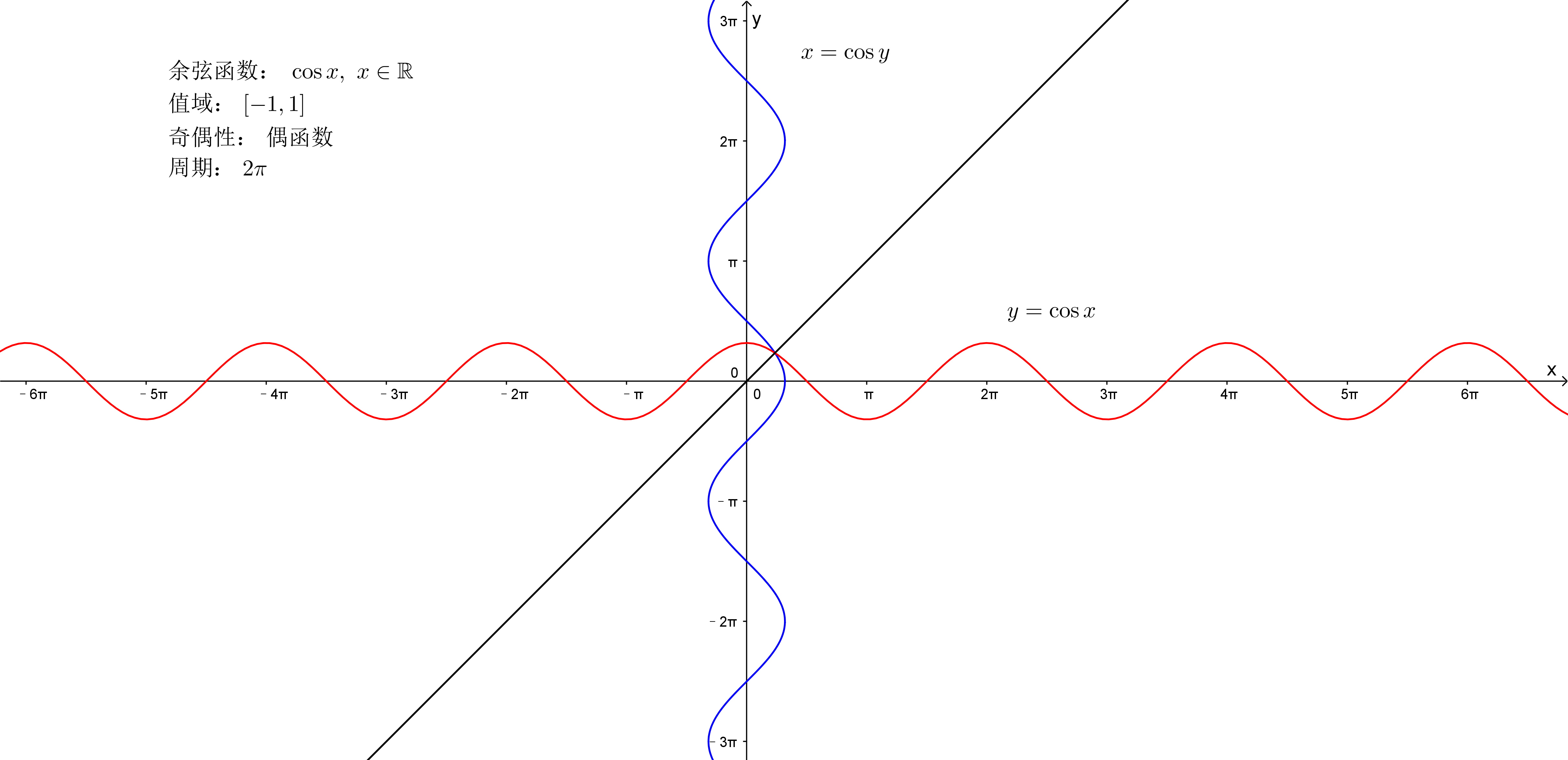
在数学中，反余弦函数是一个非常基础的函数，其函数图像常常被用来理解和掌握反余弦函数的性质。接下来，我们将详细介绍反余弦函数的图像以及它的特性。

一、反余弦函数的定义

反余弦函数，又称为反正弦函数的逆函数，常用于解析与三角函数有关的几何问题。反余弦函数的定义域是0到π之间，因此它可以在几何和工程问题中解决有关角度的精确问题。

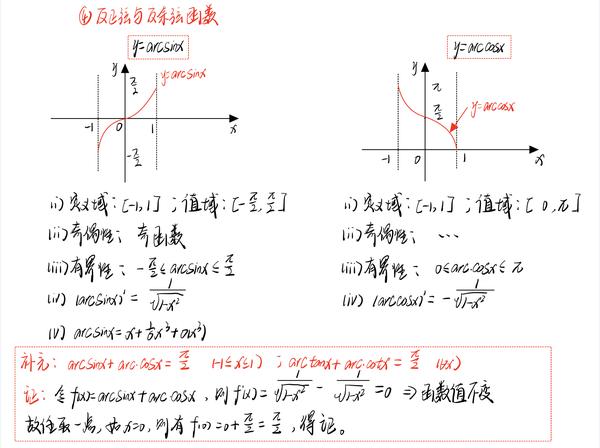
二、反余弦函数的图像

反余弦函数的图像是一条单调递减的曲线，在x轴上从0开始，一直递增到π，而y轴上的值域则是-1到1之间。这意味着在每一个角度值下，反余弦函数都有一个对应的正弦值或余弦值。

三、反余弦函数图像的特性


周期性：反余弦函数是周期性函数，周期为2π。这意味着在图像上，每隔2π的间隔，图像就会重复一次。
奇偶性：反余弦函数是偶函数，即当x取相反数时，函数值不变。这意味着在图像上，对于每一个正的x值，都有一个对应的负的x值，它们对应的y值是相同的。
渐近性：当x趋近于无穷大时，反余弦函数的值趋近于π/2或-π/2。这意味着在图像上，随着x值的增大，y值会逐渐接近于正负90度。

四、应用场景

反余弦函数在数学、物理和工程等领域都有广泛的应用。例如，在几何学中，我们可以通过反余弦函数计算两线段之间的夹角；在物理中，它常用于求解机械、电气和电子工程问题中的角度和力等参数。

总的来说，理解反余弦函数的图像及其特性是掌握该函数的基础和关键。希望本文能够帮助读者更好地理解反余弦函数的性质和应用场景。