一、文章标题


log函数


二、文章内容

在数学中，log函数是一个非常重要的概念，它被广泛应用于各种领域，包括科学、工程、计算机科学等。在本文中，我们将介绍log函数的基本概念、性质和用途。


log函数的基本概念

log函数是一个对数函数，用来表示以某个数为底，另一个数是该数的多少次方。对数函数的定义可以表述为：如果存在一个数a（a>0，a≠1），使得a的n次方等于另一个数b（b>0），那么n就叫做以a为底b的对数，记作logab。


log函数的性质

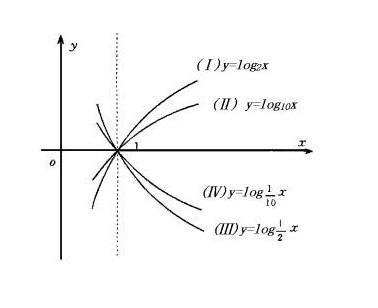
（1）单调性：对于底数大于1的对数函数，它是单调递增的；对于底数在0和1之间的对数函数，它是单调递减的。

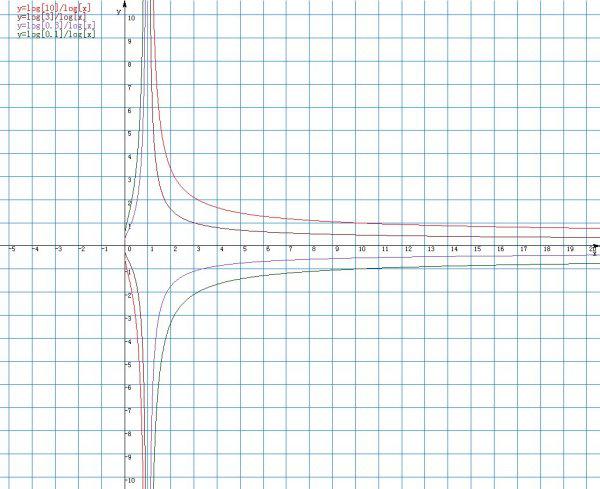
（2）换底公式：对于任意正数a（a≠1）和b（b>0），有logab=lna/lnb的换底公式。

（3）基本运算：log函数具有基本的四则运算性质，如加减乘除等。同时，它还具有对数运算法则，如乘积的对数等于对数的和等。


log函数的用途

（1）在数学中，log函数被用来解决各种问题，如解方程、求导数等。

（2）在计算机科学中，log函数常常被用来处理各种数据问题，如计算数据的大小、计算存储空间等。同时，在计算机编程中，也常常需要使用对数函数来进行各种计算。

（3）在经济学中，log函数被用来描述许多经济现象和规律，如人口增长、经济增势等。通过log函数的拟合和分析，我们可以更好地了解经济现象和规律的本质和特点。

总之，log函数是一个非常重要的数学概念，它被广泛应用于各种领域中。了解log函数的基本概念、性质和用途，可以帮助我们更好地理解和应用它。