方差的意义
一、方差的概念
方差（Variance）是一种数学统计上的重要概念，它用来表示一组数值中各数据与这组数值的平均数之差的平方的算术平均数。换句话说，它度量了数值之间的变化或离散程度。在科学研究和数据分析中，方差扮演着至关重要的角色。


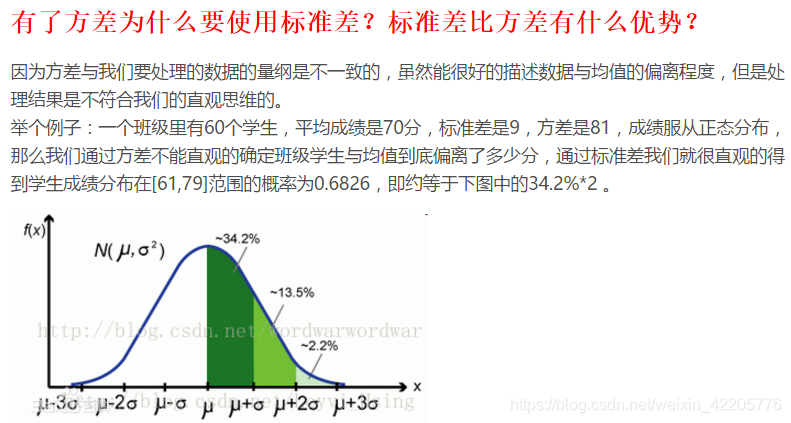
二、方差的计算
方差的计算公式为：每个数值减去平均数的差值的平方，然后除以数据的个数。这个计算过程可以有效地帮助我们理解数据的分布情况，以及数据与平均数之间的差异程度。


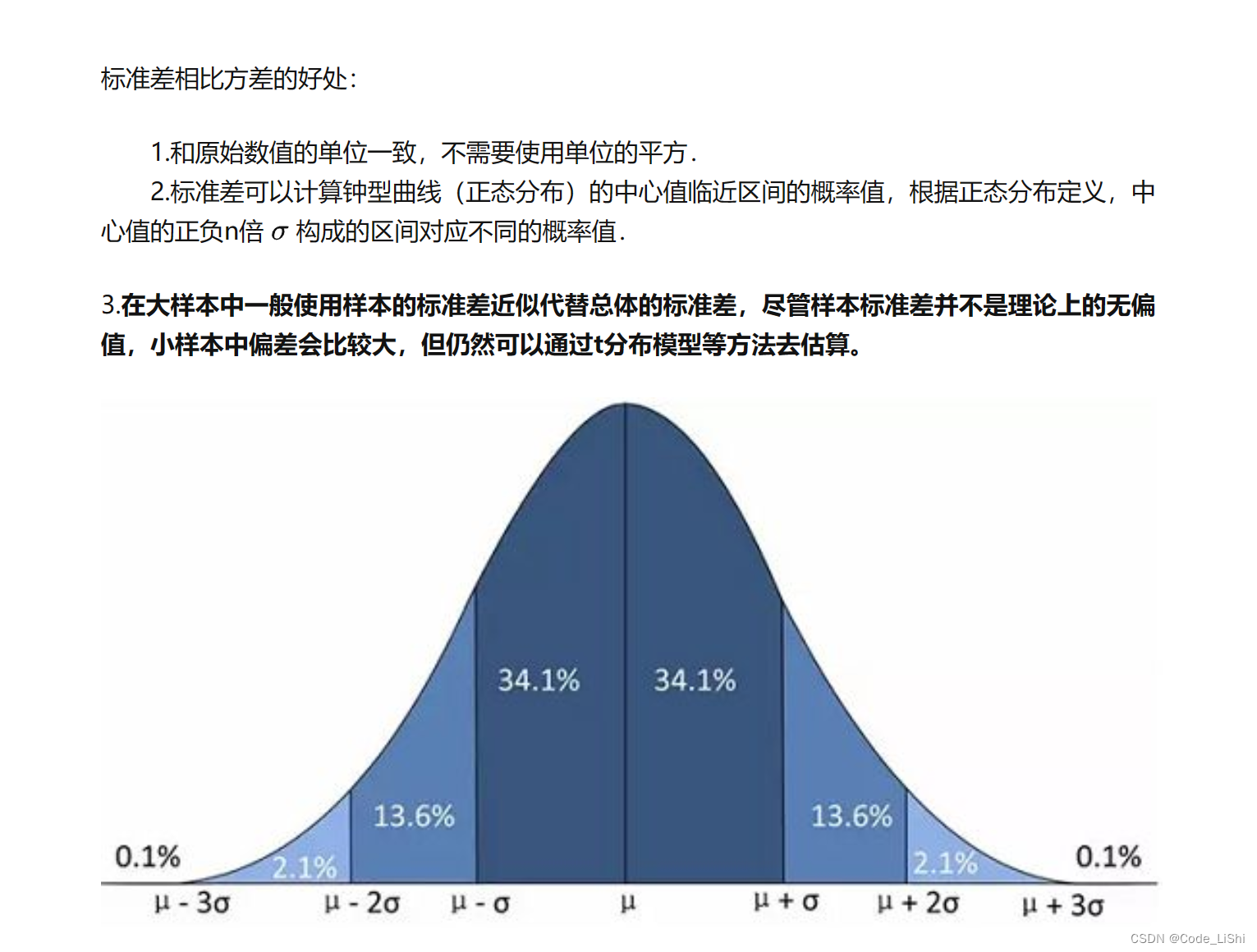
三、方差的意义
1. 描述数据的离散程度
方差可以有效地描述一组数据的离散程度。如果方差大，那么这组数据中的数值之间的差异就大；反之，如果方差小，那么这组数据中的数值之间的差异就小。因此，我们可以通过计算方差来了解数据的分布情况。

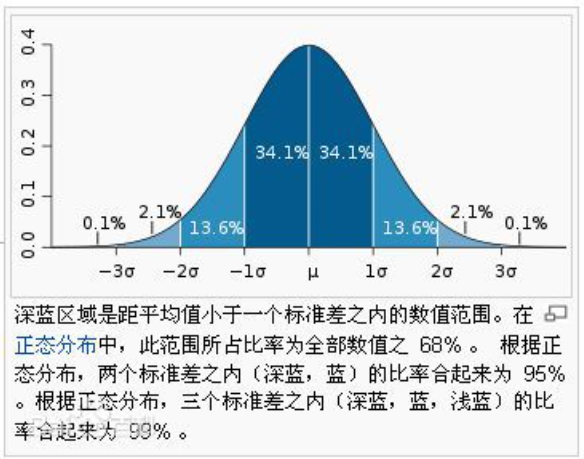
2. 数据分析的基础工具
在统计学和数据分析中，方差是一种非常重要的工具。我们可以利用方差进行数据的分析、预测、推断等操作，以此来获得关于数据的更深入的信息。同时，我们也可以利用方差来进行实验设计和抽样分析，以便更有效地进行数据采集和处理。

3. 在实际问题中的应用
在许多实际问题中，方差都有着广泛的应用。例如，在质量控制和风险评估中，我们可以利用方差来度量产品质量的变化情况以及风险的分散程度；在投资和金融领域中，我们可以通过计算资产收益的方差来了解其投资风险等。

四、总结
总的来说，方差是一种重要的数学统计概念，它不仅能够帮助我们了解数据的分布情况和变化情况，还能帮助我们进行数据分析、预测和推断等操作。因此，掌握方差的计算方法和理解其意义对于从事数据分析和统计学研究的人来说是至关重要的。