曲线拟合
概述
在数学、统计、数据分析等许多领域，我们经常需要使用曲线拟合来描述或预测一组数据的变化趋势。曲线拟合是一种数学方法，它通过选择适当的数学函数来描述一组数据点之间的关系。本文将详细介绍曲线拟合的基本概念、方法以及应用场景。


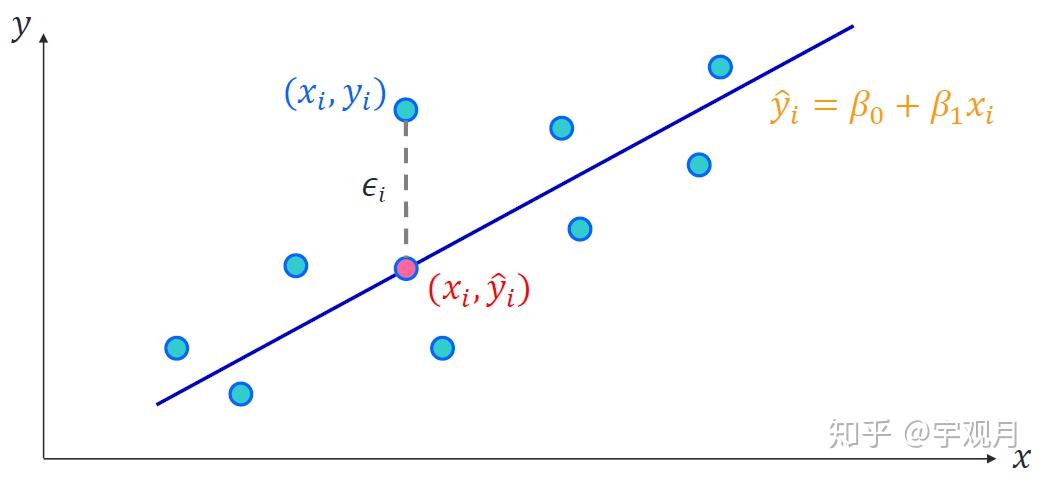
什么是曲线拟合
曲线拟合是一种通过数学方法将一组数据点拟合成一条平滑曲线的技术。在这个过程中，我们通常选择一个数学函数，然后通过调整函数的参数来使函数尽可能地接近数据点。这个过程通常使用最小二乘法等优化算法来实现。


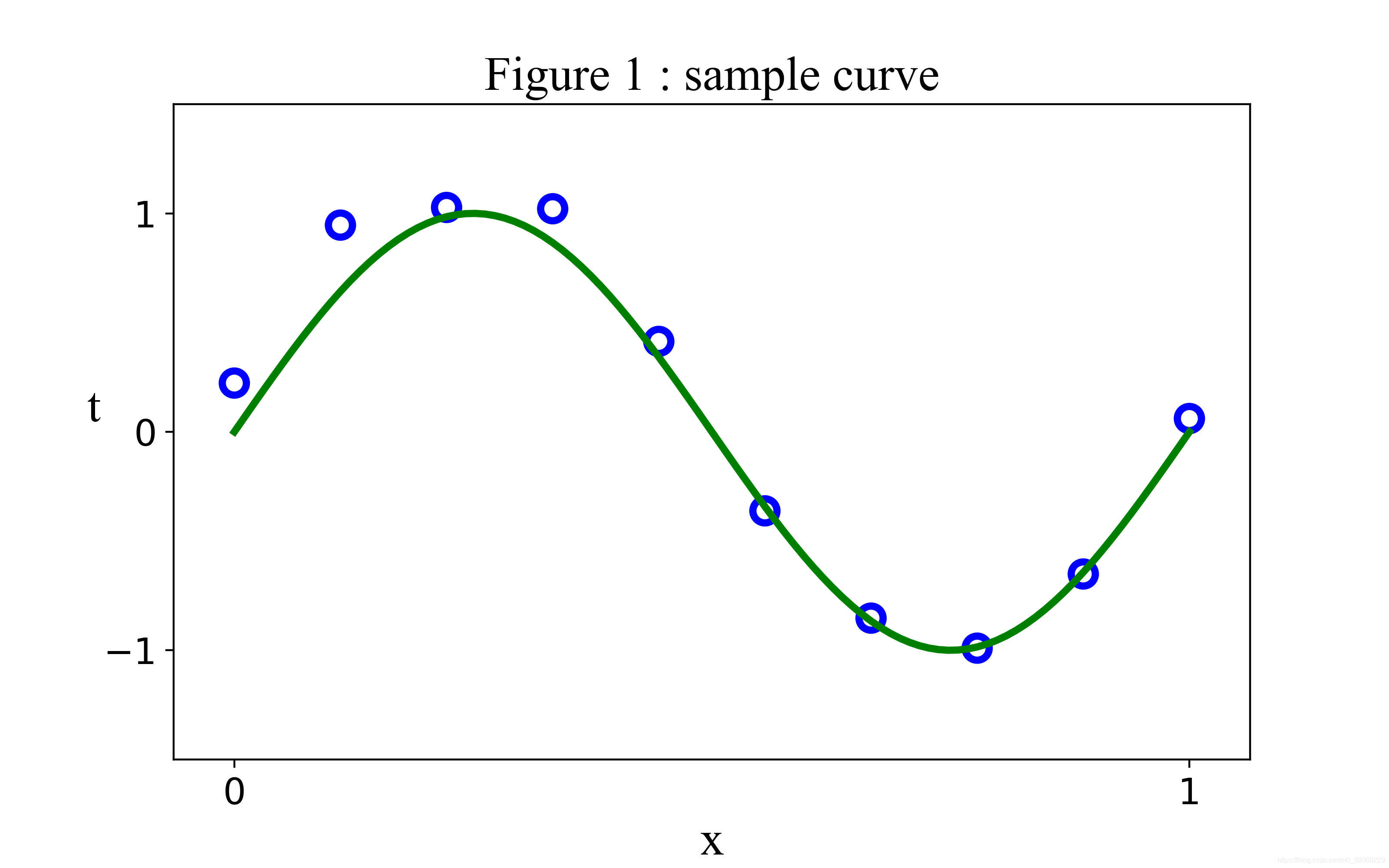
曲线拟合的方法
曲线拟合的方法有很多种，常见的包括线性回归、多项式回归、指数回归等。这些方法各有优缺点，适用于不同的数据类型和场景。


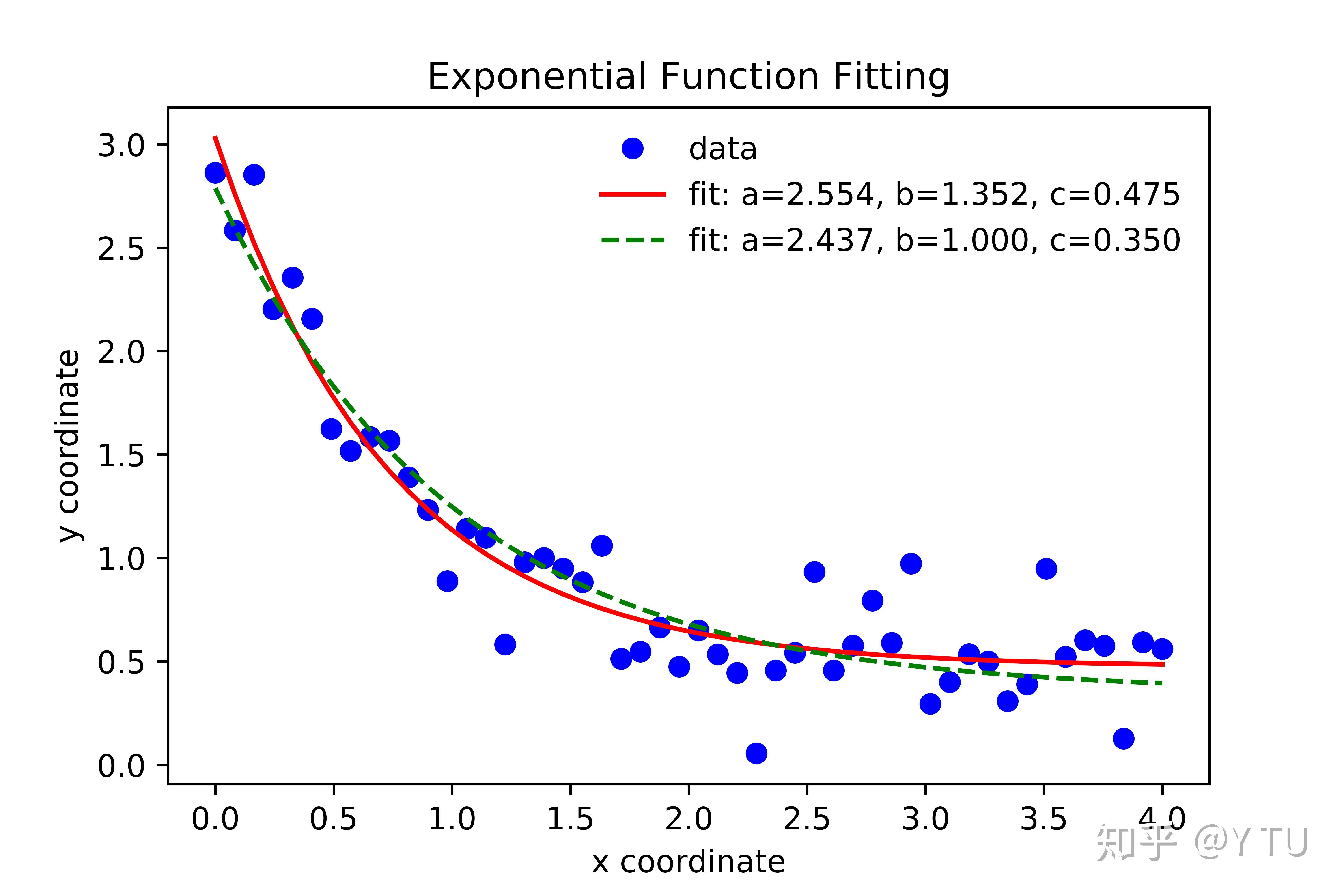
线性回归：线性回归是最简单的曲线拟合方法之一，它使用一条直线来描述数据点的变化趋势。线性回归的优点是简单易懂，计算效率高，但它的缺点是只能描述线性关系，对于非线性关系则无法准确描述。
多项式回归：多项式回归是一种通过选择一个多项式函数来描述数据点的方法。多项式回归可以描述更复杂的非线性关系，但需要注意的是多项式阶数的选择要适中，否则可能出现过拟合或欠拟合的问题。
指数回归：指数回归适用于描述一组随时间变化且呈现指数增长或衰减的数据点。指数回归通常用于生物、医学、经济等领域的研究。

曲线拟合的应用场景
曲线拟合在许多领域都有广泛的应用，如气象、生物医学、经济分析等。在气象领域中，通过分析气温和湿度的变化规律可以建立预测模型，对未来气候变化进行预测。在生物医学领域中，可以通过曲线拟合的方法来分析生物指标（如血压、血糖）的变化趋势并发现疾病的潜在风险。此外，在市场营销和经济分析中也有广泛应用。

总之，掌握和应用好曲线拟合方法不仅可以为数据分析和处理提供强大的工具和手段还可以更好地预测未来的趋势和规律提高工作效率和质量在数据驱动的现代社会具有重要的作用和意义。