一、标题：深入了解Float（浮点数）的适用范围


在现代编程语言中，数据类型占据了非常重要的一部分，浮点数作为其基础元素之一，应用在科学计算、图形处理、金融计算等众多领域。本文将深入探讨浮点数（float）的适用范围。


二、正文内容

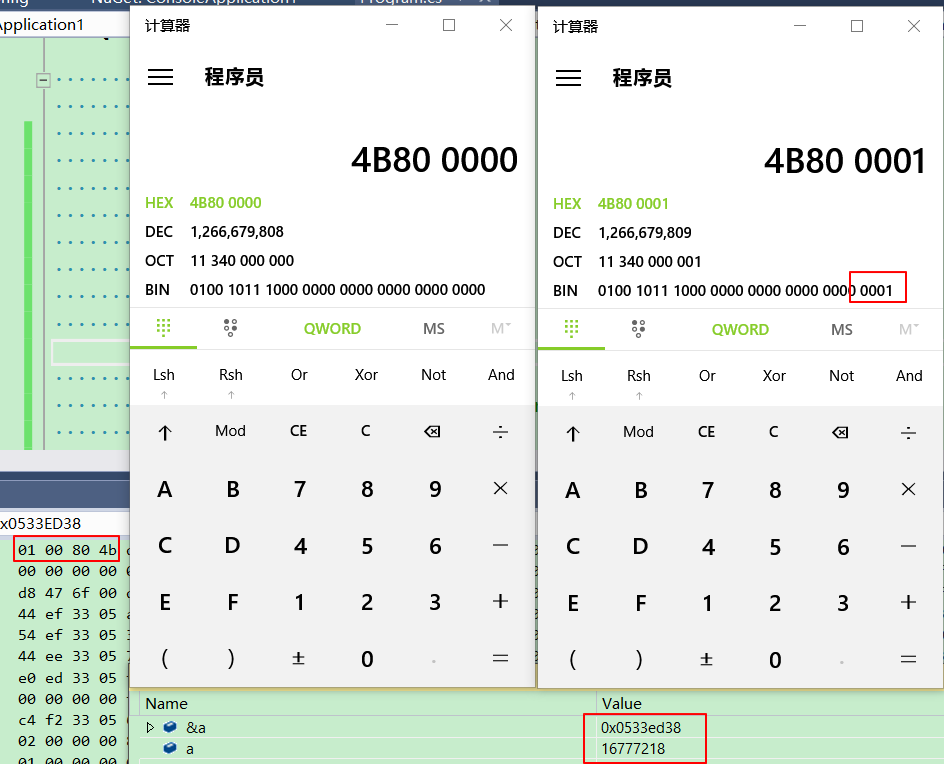
1. 浮点数的定义与特性

浮点数是一种用于表示实数的数据类型，实数也就是有整数部分和小数部分的数。其关键特征是可以准确地表示出许多与日常使用相关联的小数数据，使得数据表示和计算的准确性得以大幅提升。

2. 浮点数的适用范围

(1) 科学计算： 例如物理学和工程学等领域需要处理大量包含小数部分的数据。使用浮点数，我们可以在高精度计算时更方便快捷。例如，在天文学和物理化学等复杂模型中，常常需要进行大量精确的数值计算。

(2) 图形处理： 在3D渲染和游戏开发等图形处理工作中，常常需要用到浮点数。通过这些数据类型可以控制色彩深度、深度缓、精细控制几何对象的精细度和光影变化等，对细节的控制大大增强了图形的视觉效果。

(3) 金融计算： 精确的小数处理对于金融应用来说是必不可少的。浮点数的高精度和小数部分的表现力在股票价格计算、外汇汇率变化等方面都有着重要应用。例如，金融分析师会使用到浮点数来计算投资回报率、资产估值等重要数据。

(4) 日常应用： 在日常生活中，我们也会经常使用到浮点数。比如我们进行购物时计算价格、计算体重指数（BMI）等，都需要用到浮点数来保证计算的准确性。

3. 总结

总的来说，浮点数的应用范围非常广泛，从科学计算到日常应用，从图形处理到金融计算，几乎涵盖了所有需要精确处理小数的领域。其精确的数值表示能力和对小数部分的良好支持，使得它成为许多复杂数据处理和计算的理想选择。

以上就是关于浮点数（float）的适用范围的详细介绍。希望这篇文章能让你对浮点数有更深入的理解和认识。